题目内容
已知曲线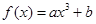 在
在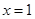 处的切线方程是
处的切线方程是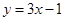 .
.
(1)求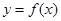 的解析式;
的解析式;
(2)求曲线过点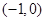 的切线方程.
的切线方程.
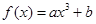 在
在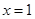 处的切线方程是
处的切线方程是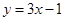 .
.(1)求
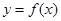 的解析式;
的解析式;(2)求曲线过点
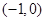 的切线方程.
的切线方程.(1) ;(2)所求切线的方程为
;(2)所求切线的方程为 或
或 .
.
 ;(2)所求切线的方程为
;(2)所求切线的方程为 或
或 .
.试题分析:(1)根据曲线在
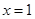 处的切线方程是
处的切线方程是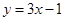 ,得到
,得到 ,进而将些等式化成关于
,进而将些等式化成关于 的方程组即可求解
的方程组即可求解 ,进而可得
,进而可得 的解析式;(2)因为本小问强调的是过点
的解析式;(2)因为本小问强调的是过点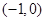 的切线问题,故需要先设切点的坐标
的切线问题,故需要先设切点的坐标 ,进而得到切线方程
,进而得到切线方程 ,再将
,再将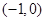 代入得
代入得 ,求解关于
,求解关于 的方程即可得出
的方程即可得出 或
或 ,进而可写出所求切线的方程.
,进而可写出所求切线的方程.(1)因为
 ,所以
,所以
又因为函数在
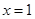 处的切线方程是
处的切线方程是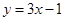
所以

所以
 6分
6分(2)设曲线过点
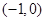 的切线的切点为
的切线的切点为
则由
 ,此时切线方程为
,此时切线方程为
因为切线过点
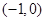
所以
 即
即
 或
或
所以所求切线的方程为
 或
或 12分.
12分.
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
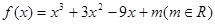 .
.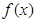 的极值(用含
的极值(用含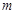 的式子表示);
的式子表示);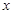 轴有3个不同交点,求
轴有3个不同交点,求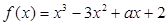 ,曲线
,曲线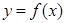 在点
在点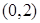 处的切线与
处的切线与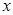 轴交点的横坐标为
轴交点的横坐标为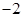 .
.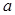 ;
;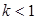 时,曲线
时,曲线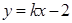 只有一个交点.
只有一个交点.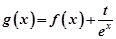 ,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;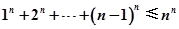 (n∈N*).
(n∈N*).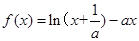 ,其中
,其中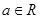 且
且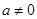 .
.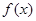 的单调性;
的单调性;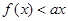 恒成立,求实数
恒成立,求实数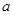 取值范围;
取值范围;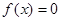 存在两个异号实根
存在两个异号实根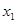 ,
,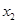 ,求证:
,求证: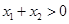
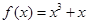 ,
,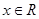 .若当
.若当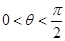 时,不等式
时,不等式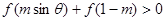 恒成立,则实数
恒成立,则实数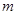 的取值范围是( )
的取值范围是( )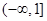
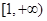
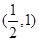
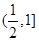
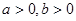 ,且函数
,且函数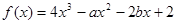 在
在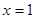 处有极值,则ab的最大值为 .
处有极值,则ab的最大值为 .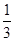 x3-
x3-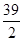 x2-40x(x>0),为使耗电量最小,则速度应定为________.
x2-40x(x>0),为使耗电量最小,则速度应定为________.