题目内容
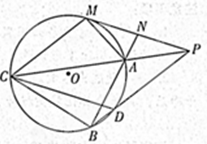
如图, ⊙O为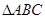 的外接圆,直线
的外接圆,直线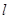 为⊙O的切线,切点为
为⊙O的切线,切点为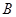 ,直线
,直线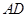 ∥
∥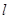 ,交
,交 于
于 ,交⊙O于
,交⊙O于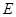 ,
,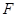 为
为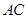 上一点,且
上一点,且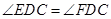 .
.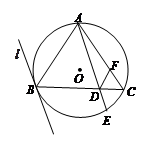
求证:(Ⅰ) ;
;
(Ⅱ)点 、
、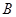 、
、 、
、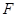 共圆.
共圆.
证明如下
解析试题分析:证明:⑴∵直线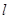 为⊙O的切线, ∴∠1=
为⊙O的切线, ∴∠1= .
. 
∵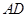 ∥
∥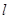 , ∴∠1=∠
, ∴∠1=∠ .
.
∴ =
= ,
,
又∵ =
= ,
,
∴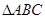 ∽
∽ .
.
∴ .
.
∴ .
.
(Ⅱ)由(Ⅰ)可知 .
.
∵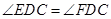 ,
,  ,
,
∴ . ∴
. ∴ 180°.
180°.
∴点 、
、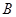 、
、 、
、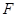 共圆.
共圆.
考点:几何证明
点评:在几何证明中,要证明关于四段线段的等式成立,只需找到四段线段所在的两个三角形,然后证明它们相似就好;而要证明四点共圆,只需证明四点形成的四边形的一对对角互补即可。

练习册系列答案
相关题目
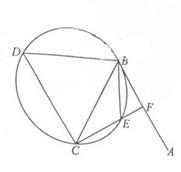
 ,延长CE交AB于点F,求△BCF外接圆的半径。
,延长CE交AB于点F,求△BCF外接圆的半径。 均在⊙O上,且
均在⊙O上,且 为⊙O的直径.
为⊙O的直径. 的值;
的值; ,
, 与
与 交于点
交于点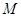 ,且
,且 、
、 为弧
为弧 的三等分点,求
的三等分点,求 的长.
的长.
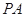 与圆
与圆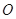 相切于点
相切于点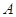 ,经过点
,经过点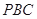 交圆
交圆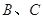 ,
,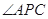 的平分线分别交
的平分线分别交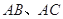 于点
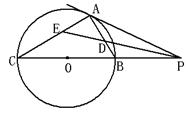
于点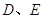 .
.
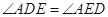 ;
;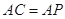 ,求
,求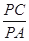 的值.
的值.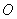 外有一点
外有一点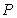 ,作圆
,作圆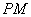 ,
,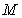 为切点,过
为切点,过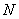 ,作割线
,作割线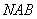 ,交圆于
,交圆于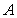 、
、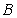 两点,连接
两点,连接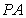 并延长,交圆
并延长,交圆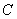 ,连续
,连续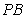 交圆
交圆 ,若
,若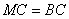 .
.
 ∽△
∽△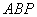 ;
;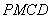 是平行四边形.
是平行四边形.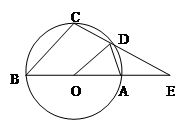
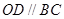 ;
;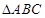 中,
中,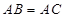 ,过点
,过点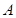 的直线与其外接圆交于点
的直线与其外接圆交于点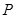 ,交
,交 延长线于点
延长线于点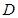 .
.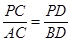 ; (2)若
; (2)若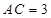 ,求
,求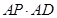
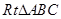 中,
中,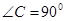 ,
,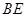 平分
平分 交
交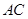 于点
于点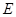 ,点
,点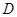 在
在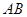 上,
上,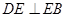 。
。 的外接圆的切线;
的外接圆的切线;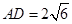 ,
,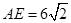 ,求
,求 的长。
的长。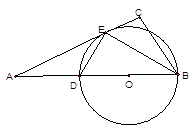
 中,
中, ,
, 平分
平分 交
交 于点
于点 ,点
,点 在
在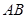 上,
上, .
.
 的外接圆的切线;
的外接圆的切线; ,求
,求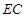 的长.
的长.