题目内容
15.下列结论正确的是( )| A. | 当x>0且x≠1时,lgx+$\frac{1}{lgx}≥2$ | |
| B. | 当x$∈(0,\frac{π}{2}]$时,sinx+$\frac{4}{sinx}$的最小值为4 | |
| C. | 当x>0时,$\sqrt{x}+\frac{1}{\sqrt{x}}$≥2 | |
| D. | 当0<x≤2时,x-$\frac{1}{x}$无最大值 |
分析 对于A,考虑0<x<1即可判断;对于B,考虑等号成立的条件,即可判断;对于C,运用基本不等式即可判断;对于D,由函数的单调性,即可得到最大值.
解答 解:对于A,当0<x<1时,lgx<0,不等式不成立;
对于B,当xx$∈(0,\frac{π}{2}]$时,sinx∈(0,1],sinx+$\frac{4}{sinx}$的最小值4取不到,由于sinx=2不成立;
对于C,当x>0时,$\sqrt{x}+\frac{1}{\sqrt{x}}$≥2$\sqrt{\sqrt{x}•\frac{1}{\sqrt{x}}}$=2,当且仅当x=1等号成立;
对于D,当0<x≤2时,x-$\frac{1}{x}$递增,当x=2时,取得最大值$\frac{3}{2}$.
综合可得C正确.
故选:C.
点评 本题考查基本不等式的运用:求最值,注意满足的条件:一正二定三等,考查运算能力,属于中档题和易错题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
5.如图是某几何体的三视图,则这个几何体是( )
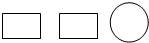

| A. | 圆柱 | B. | 球 | C. | 圆锥 | D. | 棱柱 |
6.先将函数$f(x)=cos(2x-\frac{π}{6})+1$的图象上所有点向右平移$\frac{π}{4}$个单位,再向上平移1个单位后得到函数y=g(x)的图象,则下列正确的是( )
| A. | f(x)的周期是$\frac{π}{2}$ | B. | $f(x+\frac{π}{12})$是奇函数 | ||
| C. | g(x)的图象关于点$(\frac{7π}{12},0)$对称 | D. | g(x)在区间$[0,\frac{π}{3}]$上单调递增 |
3.函数y=kx2-4x-8在区间[5,10]上是减少的,在实数k的取值范围是( )
| A. | (-$∞,\frac{1}{5}$)∪[$\frac{2}{5},+∞$] | B. | [0,$\frac{1}{5}$] | C. | (0,$\frac{1}{5}$] | D. | (-$∞,\frac{1}{5}$] |
5.已知f(x)=$\left\{\begin{array}{l}(2a-1)x+4a,x<1\\-x+1,x≥1\end{array}$是定义在R上的减函数,则a的取值范围是( )
| A. | $[\frac{1}{6},\frac{1}{2})$ | B. | $[\frac{1}{3},\frac{1}{2}]$ | C. | $(\frac{1}{6},\frac{1}{2}]$ | D. | $[\frac{1}{3},\frac{1}{2}]$ |