题目内容
已知函数![]() =
=![]() ,
,![]() .
.
(Ⅰ)求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(Ⅱ)是否存在实数![]() ,对任意给定的
,对任意给定的![]() ,在区间
,在区间![]() 上都存在两个不同的
上都存在两个不同的![]() ,使得
,使得![]() 成立.若存在,求出
成立.若存在,求出![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(Ⅲ)给出如下定义:对于函数![]() 图象上任意不同的两点
图象上任意不同的两点![]() ,如果对于函数
,如果对于函数![]() 图象上的点
图象上的点![]() (其中
(其中![]() 总能使得
总能使得![]() 成立,则称函数具备性质“
成立,则称函数具备性质“![]() ”,试判断函数
”,试判断函数![]() 是不是具备性质“
是不是具备性质“![]() ”,并说明理由.
”,并说明理由.
解:(Ⅰ)![]()
![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,且
上单调递减,且![]()
![]() 的值域为
的值域为![]() ………………3分
………………3分
(Ⅱ)令![]() ,则由(Ⅰ)可得
,则由(Ⅰ)可得![]() ,原问题等价于:对任意的
,原问题等价于:对任意的![]()
![]() 在
在![]() 上总有两个不同的实根,故
上总有两个不同的实根,故![]() 在
在![]() 不可能是单调函数 …………………5分
不可能是单调函数 …………………5分
![]()
![]()
当![]() 时,
时, ![]() ,.s
,.s ![]() 在区间
在区间![]() 上递减,不合题意
上递减,不合题意
当![]() 时,
时, ![]() ,
,![]() 在区间
在区间![]() 上单调递增,不合题意
上单调递增,不合题意
当![]() 时,
时, ![]() ,
,![]() 在区间
在区间![]() 上单调递减,不合题意
上单调递减,不合题意
当![]() 即
即![]() 时,
时, ![]() 在区间
在区间![]() 上单调递减;
上单调递减; ![]() 在区间
在区间![]() 上单递增,由上可得
上单递增,由上可得![]() ,此时必有
,此时必有![]() 的最小值小于等于0 而由
的最小值小于等于0 而由![]() 可得
可得![]() ,则
,则![]()
综上,满足条件的![]() 不存在。………………………..8分
不存在。………………………..8分
(Ⅲ)设函数![]() 具备性质“
具备性质“![]() ”,即在点
”,即在点![]() 处的切线斜率等于
处的切线斜率等于![]() ,不妨设
,不妨设![]() ,则
,则![]() ,而
,而![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,
,
故有![]() ………………10分
………………10分
即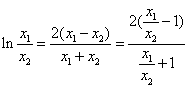 ,令
,令![]() ,则上式化为
,则上式化为![]() ,
,
………………12分
令![]()
![]() ,则由
,则由![]() 可得
可得![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,即方程
,即方程![]() 无解,所以函数
无解,所以函数![]() 不具备性质“
不具备性质“![]() ”. ……………………14分
”. ……………………14分

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|