题目内容
【题目】曲线![]() ,直线
,直线![]() 关于直线
关于直线![]() 对称的直线为
对称的直线为![]() ,直线
,直线![]() ,
,![]() 与曲线
与曲线![]() 分别交于点
分别交于点![]() 、
、![]() 和
和![]() 、
、![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)当![]() 变化时,试问直线
变化时,试问直线![]() 是否恒过定点?若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
是否恒过定点?若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
【答案】(Ⅰ)见证明;(Ⅱ)见解析
【解析】
(Ⅰ)设直线![]() 上任意一点
上任意一点![]() 关于直线
关于直线![]() 对称点为
对称点为![]() ,利用
,利用![]() 与
与![]() 关于直线
关于直线![]() 对称可得关系
对称可得关系![]() ,代入斜率乘积即可得到
,代入斜率乘积即可得到![]() 的值;
的值;
(Ⅱ)设出![]() ,
,![]() 的坐标,分别联立两直线方程与椭圆方程,求出
的坐标,分别联立两直线方程与椭圆方程,求出![]() ,
,![]() 的坐标,进一步求出
的坐标,进一步求出![]() 所在直线的斜率,写出直线方程的点斜式,整理后由直线系方程可得当
所在直线的斜率,写出直线方程的点斜式,整理后由直线系方程可得当![]() 变化时,可得直线
变化时,可得直线![]() 过定点.
过定点.
(Ⅰ)证明:设直线![]() 上任意一点
上任意一点![]() 关于直线
关于直线![]() 对称点为
对称点为![]() ,
,
直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由![]() 得
得![]() ①,
①,
由![]() ,得
,得![]() ②,
②,
由①②得![]() ,
,
![]() ;
;
(Ⅱ)设点![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,
可得![]() 或
或![]() ,
,
即![]() ,
,
由![]() ,可将
,可将![]() 换为
换为![]() ,
,
可得![]() ,
,
![]() ,
,
即直线![]() :
:![]() ,
,
可得![]()
![]() ,
,
即为![]() ,
,
则当![]() 变化时,直线
变化时,直线![]() 过定点
过定点![]() .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数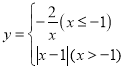 的图象与性质.列表:
的图象与性质.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
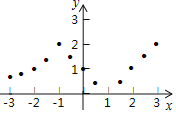
(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
(2)研究函数并结合图象与表格,回答下列问题:
①点![]() ,
,![]() ,
,![]() ,
,![]() 在函数图象上,
在函数图象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②当函数值![]() 时,求自变量x的值;
时,求自变量x的值;
③在直线![]() 的右侧的函数图象上有两个不同的点
的右侧的函数图象上有两个不同的点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直线![]() 与函数图象有三个不同的交点,求a的取值范围.
与函数图象有三个不同的交点,求a的取值范围.
【题目】某班数学兴趣小组对函数![]() 的图象和性质将进行了探究,探究过程如下,请补充完整.
的图象和性质将进行了探究,探究过程如下,请补充完整.
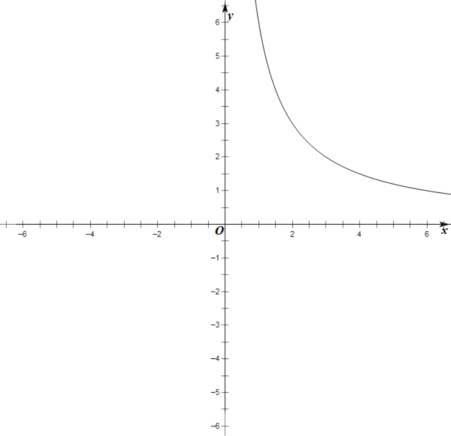
(1)自变量![]() 的取值范围是除
的取值范围是除![]() 外的全体实数,
外的全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() _________;
_________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象,写出一条函数性质;
(4)进一步探究函数图象发现:
①函数图象与![]() 轴交点情况是________,所以对应方程
轴交点情况是________,所以对应方程![]() 的实数根的情况是________;
的实数根的情况是________;
②方程![]() 有_______个实数根;
有_______个实数根;
③关于![]() 的方程
的方程![]() 有
有![]() 个实数根,
个实数根,![]() 的取值范围是________.
的取值范围是________.
【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否在犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关?说明你的理由.下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005] | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)![]()