题目内容
若a>b>0,求证: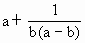 的最小值为3.
的最小值为3.
答案:
解析:
解析:
|
证:∵a>b>0,∴a-b>0.a+ |

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
题目内容
若a>b>0,求证: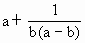 的最小值为3.
的最小值为3.
|
证:∵a>b>0,∴a-b>0.a+ |

 教材全解字词句篇系列答案
教材全解字词句篇系列答案