题目内容
如图，偶函数f(x)的图像形如字母M,奇函数g（x）的图像形如字母N，若方程
的实根个数分别为a，b，c，d，则a＋b＋c＋d＝( )
| A．27 | B．30 | C．33 | D．36 |
B
解析试题分析：因为偶函数f(x)的图像形如字母M,奇函数g（x）的图像形如字母N，由
.因为
.有三个根， 
所以有三个根，以及另两个根的绝对值大于1小于2，所以不存在，故
.由
，同上所以有三个根，另两个根的绝对值大于1小于2，所以有六个根，故
.由
，同上共有9个根，故
. 由
，也共有9个根，故
.所以
.故选B.
考点：1.函数的奇偶性.2.函数图像的应用.
练习册系列答案
阅读快车系列答案
相关题目
函数f(x)=x2+lnx
4的零点所在的区间是（ ）
| A．(0,1) | B．(1,2) | C．(2,3) | D．(3,4) |
某工厂产生的废气经过过滤后排放，排放时污染物的含量不得超过1%．己知在过滤过程中废气中的污染物数量尸（单位：毫克／升）与过滤时间t（单位：小时）之间的函数关系为：P=P0e－kt，（k，P0均为正的常数）．若在前5个小时的过滤过程中污染物被排除了90%．那么，至少还需（ ）时间过滤才可以排放．
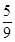A． 小时 | B． 小时 | C．5小时 | D．10小时 |
已知函数
的零点依次为
，则（ ）
A． | B． | C． | D． |
，则( )
A． | B． | C． | D． |
已知函数f(x)=2mx2-2(4-m)x+1,g(x)=mx,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数m的取值范围是( )
| A．(0,2) | B．(0,8) | C．(2,8) | D．(-∞,0) |
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x,y应为( )
| A．x=15,y=12 | B．x=12,y=15 |
| C．x=14,y=10 | D．x=10,y=14 |
若lga+lgb=0(其中a≠1,b≠1),则函数f(x)=ax与g(x)=bx的图象( )
| A．关于直线y=x对称 | B．关于x轴对称 |
| C．关于y轴对称 | D．关于原点对称 |
下列区间中，函数f(x)＝|ln(2－x)|在其上为增函数的是( )
| A．(－∞，1] | B． |
C． | D．[1,2) |