题目内容

3．若函数$f（x）=\frac{x^2}{（2x+1）（x+a）}$的图象关于y轴对称，则a=$-\frac{1}{2}$．

分析 由题意可得函数f（x）为偶函数，函数f（x）的定义域关于原点对称，从而求得a的值．

解答 解：由于函数$f（x）=\frac{x^2}{（2x+1）（x+a）}$的图象关于y轴对称，故该函数为偶函数，
故函数f（x）的定义域关于原点对称，故a=-$\frac{1}{2}$，
故答案为：-$\frac{1}{2}$．

点评 本题主要考查偶函数的图象特征，偶函数的定义域关于原点对称，属于基础题．

练习册系列答案
相关题目
15．已知${∫}_{0}^{2}$exdx=e2-1，则${∫}_{0}^{2}$3exdx等于（　　）
A．6e2-6B．3e2-3C．ex-1D．e2-1
14．已知函数f（x）=$\left\{\begin{array}{l}{{a}^{x}-1，x≤0}\\{f（x-1）+1，x＞0}\end{array}\right.$（a＞0，a≠1），把函数g（x）=f（x）-x的零点按照从小到大的顺序排成一个数列{an}，则a2016的值为（　　）
A．2008B．2015C．2016D．4032
11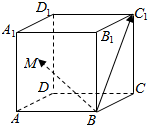．如图，在棱长为1的正方体ABCD-A1B1C1D1中，点M是左侧面ADD1A1上的一个动点，满足$\overrightarrow{B{C}_{1}}$•$\overrightarrow{BM}$=1，则$\overrightarrow{B{C}_{1}}$与$\overrightarrow{BM}$的夹角的最大值为（　　）
A．30°B．45°C．60°D．75°
18．已知圆C：x2+y2-2x-4y+1=0．
（Ⅰ）求过点M（3，1）的圆C的切线方程；
（Ⅱ）若直线l：ax-y+4=0与圆C相交于A，B两点，且弦AB的长为$2\sqrt{3}$，求a的值．
8．已知a2+b2+c2=1，则ab+bc+ac的最大值为1，最小值为-$\frac{1}{2}$．
15．a=log0.76，b=60.7，c=0.70.6，则a，b，c的大小关系为（　　）
A．a＞b＞cB．c＞a＞bC．b＞a＞cD．b＞c＞a
12．已知全集R，集合M={x|x＞1}，N={x||x|≤2}，则（∁RM）∩N等于（　　）
A．（-2，1]B．[-2，1）C．[-2，1]D．[1，2]
13．函数f（x）=x-（$\frac{1}{3}$）x+a的零点在区间（1，+∞）上，则实数a的取值范围是a＜-$\frac{2}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网