题目内容
已知f(n)=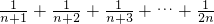 ,则f(n+1)=
,则f(n+1)=
- A.f(n)++

- B.f(n)++
 +
+
- C.f(n)-

- D.f(n)+
 -
-
D
分析:有题意得,f(n)共有n项且各项的分母从n+1变到2n,故得到f(n+1)的代数式,再用f(n)表示.
解答:∵
∴
 +…+
+…+
= +
+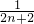
=
=f(n)+
∴故选D
点评:本题观察式子f(n)的特点,找出项数和项的变化规律,求出f(n+1),再与f(n)对比用其表示.
分析:有题意得,f(n)共有n项且各项的分母从n+1变到2n,故得到f(n+1)的代数式,再用f(n)表示.
解答:∵

∴

 +…+
+…+
=
 +
+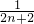
=

=f(n)+

∴故选D
点评:本题观察式子f(n)的特点,找出项数和项的变化规律,求出f(n+1),再与f(n)对比用其表示.

练习册系列答案
相关题目
 f(k+1)能被36整除
f(k+1)能被36整除