题目内容
17．某班同学参加初中毕业考试的成绩如下：| 分数 | [0，20） | [20，40） | [40，60） | [60，80） | [80，100） |
| 人数 | 2 | 1 | 8 | 36 | 13 |
| A． | 0.10 | B． | 0.15 | C． | 0.35 | D． | 0.60 |
分析 根据频率分布表中的数据，利用频率=$\frac{频数}{样本容量}$，即可求出结论．
解答 解：根据频率分布表，得；
该班学生成绩在[20，60）内的频率是$\frac{1+8}{2+2+8+36+13}$=0.15．
故选：B．
点评 本题考查了频率分布表的应用问题，也考查了频率、频数与样本容量的应用问题，是基础题目．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
8．
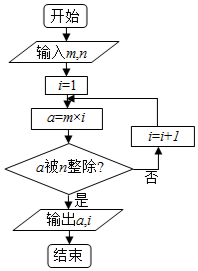当m=4，n=3时，运行如图所示的程序框图，将输出的a、i代入二项式（x2-$\frac{i}{x}$）a中，则此二项式的展开式中含x3项的系数为（ ）
当m=4，n=3时，运行如图所示的程序框图，将输出的a、i代入二项式（x2-$\frac{i}{x}$）a中，则此二项式的展开式中含x3项的系数为（ ）| A． | 37${C}_{12}^{7}$ | B． | 38${C}_{12}^{8}$ | C． | -33${C}_{12}^{3}$ | D． | -37${C}_{12}^{5}$ |
12．函数y=log2（x+1）+1（x＞1）的反函数为（ ）
| A． | y=2x-1+1（x＞2） | B． | y=2x+1+1（x＞0） | C． | y=2x-1-1（x＞2） | D． | y=2x+1-1（x＞0） |
2．双曲线M：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左、右焦点是Fl，F2，抛物线N：y2=2px（p＞0）的焦点为F2，点P是双曲线M与抛物线N的一个交点，若PF1的中点在y轴上，则该双曲线的离心率为（ ）
| A． | $\sqrt{3}$+1 | B． | $\sqrt{2}$+1 | C． | $\frac{\sqrt{3}+1}{2}$ | D． | $\frac{\sqrt{2}+1}{2}$ |