题目内容
集合P={(x,y)|x+y=-1},Q={(x,y)|x-y=3},则P∩Q=________.
{(1,-2)}
分析:根据题意,P∩Q即由集合P={(x,y)|x+y=-1},Q={(x,y)|x-y=3},表示的直线的交点,可得 ,解之即可得出答案.
,解之即可得出答案.
解答:由集合P={(x,y)|x+y=-1},Q={(x,y)|x-y=3},
∴ ,解得
,解得 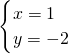 ,
,
∴P∩Q={(1,-2)},
故答案为:{(1,-2)}.
点评:本题考查的知识点是交集及其运算,其中根据二元一次方程组的解法,求出方程组x+y=-1,且x-y=3的解是解答本题的关键,另外醒本题的答案是一个点集,易错当成数集而得到错误答案{1,-2}.
分析:根据题意,P∩Q即由集合P={(x,y)|x+y=-1},Q={(x,y)|x-y=3},表示的直线的交点,可得
 ,解之即可得出答案.
,解之即可得出答案.解答:由集合P={(x,y)|x+y=-1},Q={(x,y)|x-y=3},
∴
 ,解得
,解得 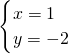 ,
,∴P∩Q={(1,-2)},
故答案为:{(1,-2)}.
点评:本题考查的知识点是交集及其运算,其中根据二元一次方程组的解法,求出方程组x+y=-1,且x-y=3的解是解答本题的关键,另外醒本题的答案是一个点集,易错当成数集而得到错误答案{1,-2}.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 ,a>0,a≠1},如果P
,a>0,a≠1},如果P Q有且只有一个元素,那么实数m的取值范围是________.
Q有且只有一个元素,那么实数m的取值范围是________.