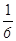题目内容
两个实习生每人加工一个零件,加工为一等品的概率分别为![]() 和
和![]() ,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个加工为一等品的概率为 .
,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个加工为一等品的概率为 .
设事件A:甲实习生加工的零件为一等品;事件B:乙实习生加工的零件为一等品,则P(A)=![]() ,P(B)=
,P(B)=![]() ,所以这两个零件中恰有一个加工为一等品的概率为:P(A
,所以这两个零件中恰有一个加工为一等品的概率为:P(A![]() )+P(
)+P(![]() B)=P(A)·P(
B)=P(A)·P(![]() )+P(
)+P(![]() )·P(B)=
)·P(B)=![]() ×(1-
×(1-![]() )+(1-
)+(1-![]() )×
)×![]() =
=![]() .
.
答案:![]()
【方法技巧】已知两个事件A、B相互独立,它们的概率分别为P(A)、P(B),则有
| 事件 | 表示 | 概率 |
| A、B同时发生 | AB | P(A)P(B) |
| A、B都不发生 |
| P( |
| A、B恰有一个发生 | (A | P(A)P( |
| A、B中至少有一个发生 | (A | P(A)P( |
| A、B中至多有一个发生 | (A ( | P(A)P( |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
两个实习生每人加工一个零件.加工为一等品的概率分别为
和
,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
| 2 |
| 3 |
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 和
和 ,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( ) B、
B、 C、
C、 D、
D、 
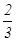 和
和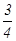 ,两个零件是 否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为
,两个零件是 否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为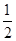 (B)
(B)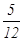 (C)
(C)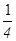 (D)
(D)