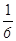题目内容
两个实习生每人加工一个零件,加工为一等品的概率分别为| 2 |
| 3 |
| 3 |
| 4 |
分析:分别记两个实习生加工一个零件为一等品的事件为A,B,则由已知可得P(A)=
,P(B)=
,且A,B相互独立,两个零件中恰有一个一等品的概率为P=1-P(
•
)=1-P(
)P(
)-P(A)P(B).
| 2 |
| 3 |
| 3 |
| 4 |
. |
| A |
. |
| B |
. |
| A |
. |
| B |
解答:解:分别记两个实习生加工一个零件为一等品的事件为A,B,
则由已知可得P(A)=
,P(B)=
,且A,B相互独立,
两个零件中恰有一个一等品的概率为P=1-P(
•
)=1-P(
)P(
)-P(A)P(B)=1-
×
-
×
=
故答案为:
.
则由已知可得P(A)=
| 2 |
| 3 |
| 3 |
| 4 |
两个零件中恰有一个一等品的概率为P=1-P(
. |
| A |
. |
| B |
. |
| A |
. |
| B |
| 1 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
| 5 |
| 12 |
故答案为:
| 5 |
| 12 |
点评:本题主要考查了相互独立事件的概率公式的求解:若A,B相互独立,则P(AB)=P(A)P(B);还利用了对立事件的概率公式,要注意该方法在解决概率问题时,若正面情况较多时,可以利用此方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
两个实习生每人加工一个零件.加工为一等品的概率分别为
和
,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
| 2 |
| 3 |
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 和
和 ,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( ) B、
B、 C、
C、 D、
D、 
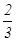 和
和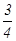 ,两个零件是 否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为
,两个零件是 否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为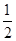 (B)
(B)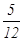 (C)
(C)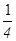 (D)
(D)