题目内容
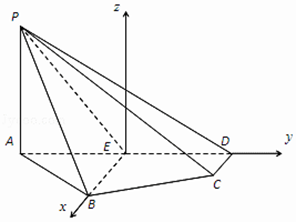
【题目】如图,在四棱锥P﹣ABCD中,侧棱PA⊥平面ABCD,E为AD的中点,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1; 
(1)求二面角C﹣PB﹣E的余弦值;
(2)在线段PE上是否存在点M,使得DM∥平面PBC?若存在,求出点M的位置,若不存在,说明理由.
【答案】
(1)解:作Ez⊥AD,以E为原点,以 ![]() ,
, ![]() 的方向分别为x轴,y轴的正方向,建立如图所示的空间直角坐标系E﹣xyz,
的方向分别为x轴,y轴的正方向,建立如图所示的空间直角坐标系E﹣xyz,
则点E(0,0,0),P(0,﹣2,2),A(0,﹣2,0),B(2,0,0),C(1,2,0),D(0,2,0).
∴ ![]() =(2,2,﹣2,),
=(2,2,﹣2,), ![]() =(﹣1,2,0),
=(﹣1,2,0), ![]() =(0,﹣2,2).
=(0,﹣2,2).
设平面PBC的法向量为 ![]() =(x,y,z),
=(x,y,z),
由 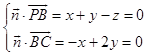 ,可取
,可取 ![]() =(2,1,3).
=(2,1,3).
设平面PBE的法向量为 ![]() =(a,b,c),
=(a,b,c),
由 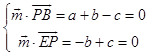 ,可取
,可取 ![]() =(0,1,1),
=(0,1,1),
∴ ![]() =
= ![]()
由图可知,二面角C﹣PB﹣E的余弦值为 ![]() .
.
(2)解:由(1)可知面PBC的法向量为 ![]() =(2,1,3),“线段PE上存在点M,使得DM∥平面PBC”等价于
=(2,1,3),“线段PE上存在点M,使得DM∥平面PBC”等价于 ![]() ;
;
∵ ![]() =(0,2,﹣2),
=(0,2,﹣2), ![]() =(0,2λ,﹣2λ),λ∈(0,1),
=(0,2λ,﹣2λ),λ∈(0,1),
则M(0,2λ﹣2,2﹣2λ), ![]() =(0,2λ﹣4,2﹣2λ).
=(0,2λ﹣4,2﹣2λ).
由 ![]() =2λ﹣4+6﹣6λ=0.
=2λ﹣4+6﹣6λ=0.
解得λ= ![]() ,
,
所以线段PE上存在点M,即PE中点,使得DM∥平面PBC.
【解析】(1)作Ez⊥AD,以E为原点,以 ![]() ,
, ![]() 的方向分别为x轴,y轴的正方向,建立如图所示的空间直角坐标系E﹣xyz,则点E(0,0,0),P(0,﹣2,2),A(0,﹣2,0),B(2,0,0),C(1,2,0),D(0,2,0).求出平面PBC的法向量、平面PBE的法向量即可得二面角C﹣PB﹣E的余弦值;(2)线段PE上存在点M,使得DM∥平面PBC”等价于
的方向分别为x轴,y轴的正方向,建立如图所示的空间直角坐标系E﹣xyz,则点E(0,0,0),P(0,﹣2,2),A(0,﹣2,0),B(2,0,0),C(1,2,0),D(0,2,0).求出平面PBC的法向量、平面PBE的法向量即可得二面角C﹣PB﹣E的余弦值;(2)线段PE上存在点M,使得DM∥平面PBC”等价于 ![]() 垂直面PBC的法向量.
垂直面PBC的法向量.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

【题目】某医疗科研项目对5只实验小白鼠体内的A、B两项指标数据进行收集和分析,得到的数据如下表:
指标 | 1号小白鼠 | 2号小白鼠 | 3号小白鼠 | 4号小白鼠 | 5号小白鼠 |
A | 5 | 7 | 6 | 9 | 8 |
B | 2 | 2 | 3 | 4 | 4 |
(1)若通过数据分析,得知A项指标数据与B项指标数据具有线性相关关系,试根据上表,求B项指标数据y关于A项指标数据x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)现要从这5只小白鼠中随机抽取3只,求其中至少有一只B项指标数据高于3的概率. 参考公式: ![]() =
= 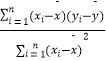 =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.