题目内容
已知函数![]() ,
,![]() .
.
(I)当函数![]() 取得最大值时,求自变量
取得最大值时,求自变量![]() 的集合;
的集合;
(II)该函数的图象可由![]() 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
解:(Ⅰ)
y=![]() cos2x+
cos2x+![]() sinxcosx+1
sinxcosx+1
=![]() (2cos2x-1)+
(2cos2x-1)+![]() +
+![]() (2sinxcosx)+1
(2sinxcosx)+1
=![]() cos2x+
cos2x+![]() sin2x+
sin2x+![]() =
=![]() (cos2x?sin
(cos2x?sin![]() +sin2x?cos
+sin2x?cos![]() )+
)+![]()
=![]() sin(2x+
sin(2x+![]() )+
)+![]()
y取得最大值必须且只需
2x+![]() =
=![]() +2kπ,k∈Z,即 x=
+2kπ,k∈Z,即 x=![]() +kπ,k∈Z.
+kπ,k∈Z.
所以当函数y取得最大值时,自变量x的集合为
{x|x=![]() +kπ,k∈Z }
+kπ,k∈Z }
(Ⅱ)将函数y=sinx依次进行如下变换:
(i)把函数y=sinx的图象向左平移![]() ,得到函数y=sin(x+
,得到函数y=sin(x+![]() )的图象;
)的图象;
(ii)把得到的图象上各点横坐标缩短到原来的![]() 倍(纵坐标不变),得到函数y=sin(2x+
倍(纵坐标不变),得到函数y=sin(2x+![]() )的图象;
)的图象;
(iii)把得到的图象上各点纵坐标缩短到原来的![]() 倍(纵坐标不变),得到函数y=
倍(纵坐标不变),得到函数y=![]() sin(2x+
sin(2x+![]() )的图象;
)的图象;
(iv)把得到的图象向上平移![]() 个单位长度,得到函数y=
个单位长度,得到函数y=![]() sin(2x+
sin(2x+![]() )+
)+![]() 的图象;综上得到函数y=
的图象;综上得到函数y=![]() cos2x+
cos2x+![]() sinxcosx+1的图象.
sinxcosx+1的图象.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 ,
, .
. ,
, 。
。 的单调区间;
的单调区间; ,曲线C与其在点
,曲线C与其在点 处的切线交于另一点
处的切线交于另一点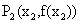 ,曲线C与其在点
,曲线C与其在点 ,线段
,线段
 (Ⅰ)(ii)的正确命题,并予以证明。
(Ⅰ)(ii)的正确命题,并予以证明。