题目内容
如图,A地到火车站共有两条路径L1和L2,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:


现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站。
(Ⅰ)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(Ⅱ)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(Ⅰ)的选择方案,求X的分布列和数学期望。
解 (Ⅰ)Ai表示事件“甲选择路径Li时,40分钟内赶到火车站”,Bi表示事件“乙选择路径Li时,50分钟内赶到火车站”,i=1,2.用频率估计相应的概率可得
P(A1)=0.1+0.2+0.3=0.6,P(A2)=0.1+0.4=0.5,
![]() P(A1) >P(A2),
P(A1) >P(A2), ![]() 甲应选择Li
甲应选择Li
P(B1)=0.1+0.2+0.3+0.2=0.8,P(B2)=0.1+0.4+0.4=0.9,
![]() P(B2) >P(B1),
P(B2) >P(B1), ![]() 乙应选择L2.
乙应选择L2.
(Ⅱ)A,B分别表示针对(Ⅰ)的选择方案,甲、乙在各自允许的时间内赶到火车站,由(Ⅰ)知![]() ,又由题意知,A,B独立,
,又由题意知,A,B独立,

![]()
X分布为

∴![]()

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
如图,A地到火车站共有两条路径L1和L2,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站.
(Ⅰ)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(Ⅱ)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(Ⅰ)的选择方案,求X的分布列和数学期望.
| 所用时间(分钟) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| L1的频率 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
| L2的频率 | 0 | 0.1 | 0.4 | 0.4 | 0.1 |
(Ⅰ)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(Ⅱ)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(Ⅰ)的选择方案,求X的分布列和数学期望.
本小题满分13分)
如图,A地到火车站共有两条路径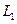 和
和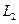 ,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
| 时间(分钟) | 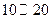 | 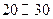 | 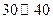 |  | 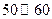 |
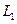 的频率 的频率 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
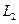 的频率 的频率 | 0 | 0.1 | 0.4 | 0.4 | 0.1 |
(Ⅰ)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(Ⅱ)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(Ⅰ)的选择方案,求X的分布列和数学期望。
如图,A地到火车站共有两条路径L1,L2,现随机抽取100位从A地到火车站的人进行调查,结果如下:
|
所用时间(min) |
10~20 |
20~30 |
30~40 |
40~50 |
50~60 |
|
选择L1人数 |
6 |
12 |
18 |
12 |
12 |
|
选择L2人数 |
0 |
4 |
16 |
16 |
4 |
(1)试估计40 min内不能赶到火车站的概率
(2)现甲有40 min时间赶往火车站,为尽最大可能在允许的时间内赶到火车站,试通过计算说明,他如何选路径
 20、如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:
20、如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下: 如图,A地到火车站共有两条路径L1,L2,现随机抽取100位从A地到火车站的人进行调查,结果如下:
如图,A地到火车站共有两条路径L1,L2,现随机抽取100位从A地到火车站的人进行调查,结果如下: