题目内容
对于在区间[m,n]上有意义的两个函数f(x)与g(x),如果对任意的x∈[m,n],均有|f(x)-g(x)|≤1,则称f(x)与g(x)在[m,n]上是接近的,否则称f(x)与g(x)在[m,n]上是非接近的.现有两个函数f1(x)=loga(x-3a)与f2(x)=(1)若f1(x)与f2(x)在给定区间[a+2,a+3]上都有意义,求a的取值范围;
(2)讨论f1(x)与f2(x)在给定区间[a+2,a+3]上是否是接近的.
答案:
解析:
提示:
解析:
| (1)由题意a>0,a≠1且a+2-3a>0
所以0<a<1. (2)|f1(x)-f2(x)|=|loga(x2-4ax+3a2)| 令|f1(x)-f2(x)|≤1 得-1≤loga(x2-4ax+3a2)≤l ① ∵ 0<a<1 又[a+2,a+3]在x=2a的右侧 ∴ g(x)=loga(x2-4ax+3a2)在[a+2,a+3]上为减函数 从而g(x)max=g(a+2)=loga(4-4a) g(x)min=g(a+3)=loga(9-6a) 于是①式成立的充要条件是 解此不等式组得0<a≤ 故当0<a≤ 当1>a> |
提示:
| 本题是考查学生创新能力的综合题,首先学生读懂新运算定义,再利用函数单调性和不等式知识才可求出. |

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目

 与
与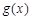 ,如果对任意
,如果对任意 ,均有
,均有 与
与 (a > 0且
(a > 0且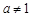 ),给定区间
),给定区间 .
. 与
与 在给定区间
在给定区间