题目内容
已知椭圆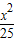
+
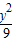上一点P到两焦点距离之积为m，则当m取最大值时，P点坐标 ．
【答案】分析：根据椭圆的定义，P到两焦点距离之和满足|PF1|+|PF2|=2a=10，由基本不等式可得：当且仅当|PF1|=|PF2|=5时，P到两焦点距离之积为m有最大值为25．由此可得m取最大值时P点坐标．
解答：解：设椭圆的左右焦点为F1、F2
根据椭圆的定义，可得|PF1|+|PF2|=2a=10
∵|PF1|•|PF2|≤[
（|PF1|+|PF2|）]2=25
当且仅当|PF1|=|PF2|=5时，P到两焦点距离之积为m有最大值为25
∴当m取最大值时，P点位于短轴的顶点，其坐标为（0，±4）
故答案为：（0，±4）
点评：本题求椭圆上动点P到两个焦点距离之积的最大值．着重考查了椭圆的定义与标准方程、基本不等式求最值等知识，属于中档题．
解答：解：设椭圆的左右焦点为F1、F2
根据椭圆的定义，可得|PF1|+|PF2|=2a=10
∵|PF1|•|PF2|≤[
（|PF1|+|PF2|）]2=25当且仅当|PF1|=|PF2|=5时，P到两焦点距离之积为m有最大值为25
∴当m取最大值时，P点位于短轴的顶点，其坐标为（0，±4）
故答案为：（0，±4）
点评：本题求椭圆上动点P到两个焦点距离之积的最大值．着重考查了椭圆的定义与标准方程、基本不等式求最值等知识，属于中档题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
=1上一点P到一个焦点的距离为3，那么点P到另一个焦点的距离为( )
+
=1上一点P到它的右准线的距离为10,则点P到它的左焦点的距离是( )
=1上一点P到椭圆的一个焦点的距离是3,则P点到另一个焦点的距离是( )
=1上一点P到椭圆的一个焦点的距离是3,则P点到另一个焦点的距离是( )
+
=1上一点P到其一个焦点的距离为3,则点P到另一个焦点的距离为( )