题目内容
已知函数f(x)=-x2+ax-lnx(a∈R).
(1)求函数f(x)既有极大值又有极小值的充要条件;
(2)当函数f(x)在[![]() ,2]上单调时,求a的取值范围.
,2]上单调时,求a的取值范围.
解:(1)∵f′(x)=-2x+a-![]() =
=![]() (x>0),
(x>0),
∴f(x)既有极大值又有极小值⇔方程2x2-ax+1=0有两个不等的正实数根x1,x2.
(3分)
∴ ,∴a>2
,∴a>2![]() ,
,
∴函数f(x)既有极大值又有极小值的充要条件是a>2![]() .(6分)
.(6分)
(2)f′(x)=-2x+a-![]() ,令g(x)=2x+
,令g(x)=2x+![]() ,
,
则g′(x)=2-![]() ,g(x)在[
,g(x)在[![]() ,
,![]() ]上递减,在(
]上递减,在(![]() ,2)上递增.(8分)
,2)上递增.(8分)
又g(![]() )=3,g(2)=
)=3,g(2)=![]() ,g(
,g(![]() )=2
)=2![]() ,
,
∴g(x)max=![]() ,g(x)min=2
,g(x)min=2![]() .(10分)
.(10分)
若f(x)在[![]() ,2]单调递增,则f′(x)≥0即a≥g(x),∴a≥
,2]单调递增,则f′(x)≥0即a≥g(x),∴a≥![]() .
.
若f(x)在[![]() ,2]单调递减,则f′(x)≤0,即a≤g(x),∴a≤2
,2]单调递减,则f′(x)≤0,即a≤g(x),∴a≤2![]() .
.
所以f(x)在[![]() ,2]上单调时,则a≤2
,2]上单调时,则a≤2![]() 或a≥
或a≥![]() .(13分)
.(13分)


练习册系列答案
相关题目
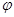 )(ω>0,0<
)(ω>0,0<
 =
= ,且a∈(0,
,且a∈(0, ),求f(a)的值.
),求f(a)的值. -a
-a +x(a>0).
+x(a>0). =
= ,求f(x)图像在x=1处的切线的方程;
,求f(x)图像在x=1处的切线的方程; 的极大值和极小值分别为m,n,证明:
的极大值和极小值分别为m,n,证明: .
.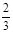 与x=1时都取得极值.
与x=1时都取得极值. ,若f(x)存在零点,则实数a的取值范围
,若f(x)存在零点,则实数a的取值范围