题目内容
(本题满分10分)已知m>1,直线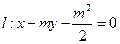 ,椭圆
,椭圆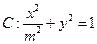 ,
,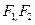 分别为椭圆
分别为椭圆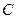 的左、右焦点.
的左、右焦点.
(Ⅰ)当直线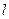 过右焦点
过右焦点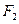 时,求直线
时,求直线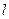
 的方程;
的方程;
(Ⅱ)设直线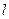 与椭圆
与椭圆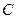 交于
交于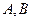 两点,
两点,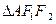 ,
,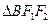 的重心分别为
的重心分别为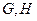 .若原点
.若原点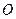 在以线段
在以线段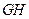 为直径的圆内,求实数
为直径的圆内,求实数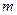 的取值范围.
的取值范围. 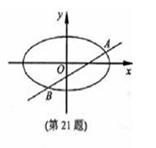
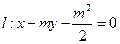 ,椭圆
,椭圆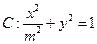 ,
,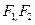 分别为椭圆
分别为椭圆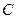 的左、右焦点.
的左、右焦点. (Ⅰ)当直线
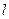 过右焦点
过右焦点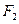 时,求直线
时,求直线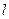
 的方程;
的方程;(Ⅱ)设直线
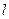 与椭圆
与椭圆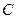 交于
交于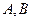 两点,
两点,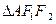 ,
,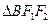 的重心分别为
的重心分别为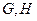 .若原点
.若原点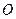 在以线段
在以线段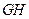 为直径的圆内,求实数
为直径的圆内,求实数 的取值范围.
的取值范围. 
(Ⅰ)
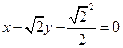
(Ⅱ)
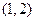
(Ⅰ)解:因为直线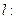
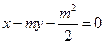 经过
经过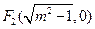 ,
,
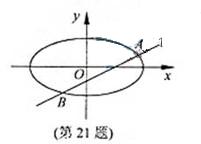
所以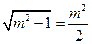 ,得
,得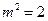 ,
,
又因为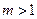 ,所以
,所以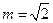 ,故直线
,故直线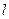 的方程为
的方程为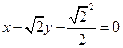 。
。
(Ⅱ)解:设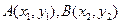 。
。
由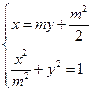 ,消去
,消去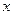 得
得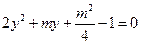
则由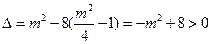 ,知
,知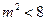 ,
,
且有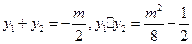 。由于
。由于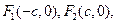 ,故
,故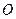 为
为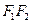 的中点,
的中点,
由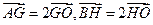 ,可知
,可知
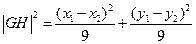
设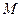 是
是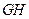 的中点,则
的中点,则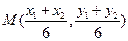 ,由题意可知
,由题意可知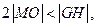
即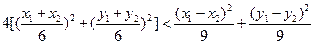
即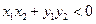
而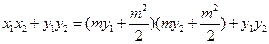
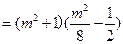
所以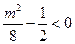
即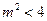
 又因为
又因为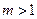 且
且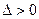
所以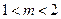 。
。
所以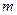 的取值范围是
的取值范围是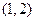 。
。
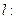
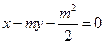 经过
经过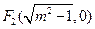 ,
,
所以
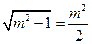 ,得
,得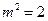 ,
,又因为
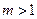 ,所以
,所以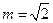 ,故直线
,故直线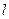 的方程为
的方程为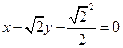 。
。(Ⅱ)解:设
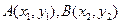 。
。
|
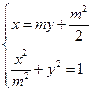 ,消去
,消去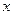 得
得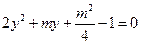
则由
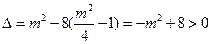 ,知
,知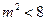 ,
,且有
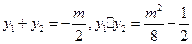 。由于
。由于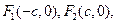 ,故
,故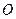 为
为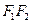 的中点,
的中点,由
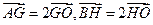 ,可知
,可知
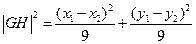
设
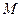 是
是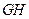 的中点,则
的中点,则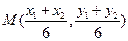 ,由题意可知
,由题意可知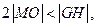
即
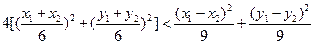
即
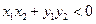
而
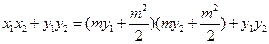
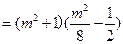
所以
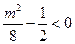
即
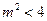
 又因为
又因为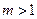 且
且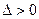
所以
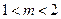 。
。所以
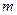 的取值范围是
的取值范围是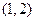 。
。
练习册系列答案
相关题目
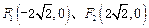 ,长轴长为6,
,长轴长为6,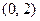 且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度.
且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度.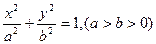 的左焦点,A(-a,0), B(0,b), 椭圆的离心率为
的左焦点,A(-a,0), B(0,b), 椭圆的离心率为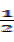 , 点D在x轴上,
, 点D在x轴上,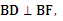 B,D,F三点确定的圆M恰好与直线l1:x+
B,D,F三点确定的圆M恰好与直线l1:x+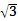 y+30相切
y+30相切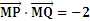 ,求直线l2的方程
,求直线l2的方程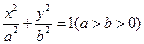 的离心率为
的离心率为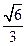 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为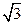 ,直线
,直线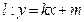 交椭圆于不同的两点
交椭圆于不同的两点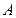 ,
,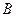
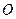 到直线
到直线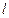 的距离为
的距离为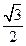 ,求
,求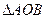 面积的最大值
面积的最大值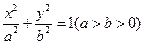 ,两个焦点分别为
,两个焦点分别为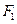 、
、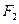 ,斜率为k的直线
,斜率为k的直线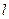 过右焦点
过右焦点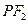 的中点恰为B。
的中点恰为B。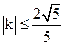 ,求椭圆C的离心率的取值范围。
,求椭圆C的离心率的取值范围。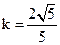 ,A、B到右准线距离之和为
,A、B到右准线距离之和为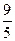 ,求椭圆C的方程。
,求椭圆C的方程。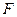 为椭圆的左焦点,
为椭圆的左焦点, 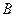 为椭圆的一个顶点,过点
为椭圆的一个顶点,过点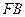 垂直的直线
垂直的直线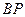 交
交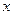 轴于
轴于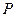 点, 且椭圆的长半轴长
点, 且椭圆的长半轴长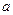 和短半轴长
和短半轴长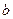 是关于
是关于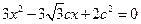 (其中
(其中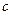 为半焦距)的两个根.
为半焦距)的两个根.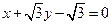 相切,试求椭圆的方程.
相切,试求椭圆的方程.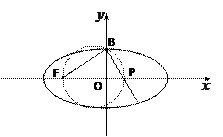
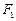 、
、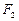 是椭圆
是椭圆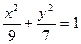 的两个焦点,
的两个焦点,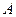 为椭圆上一点,且∠
为椭圆上一点,且∠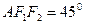 ,则Δ
,则Δ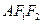 的面积为( )
的面积为( ) 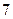
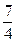
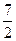

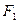 、
、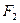 分别是椭圆
分别是椭圆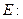
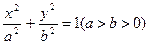 的左、右焦点,过
的左、右焦点,过 的直线
的直线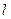 与
与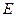 相交于
相交于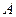 、
、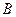 两点,且
两点,且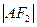 、
、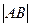 、
、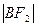 成等差数列.
成等差数列.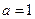 ,求
,求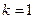 ,设点
,设点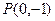 满足
满足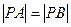 ,求椭圆
,求椭圆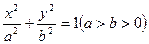 的右焦点为F,C为椭圆短轴的端点,向量
的右焦点为F,C为椭圆短轴的端点,向量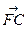 绕F点顺时针旋转
绕F点顺时针旋转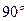 后得到向量
后得到向量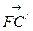 ,其中
,其中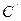 点恰好落在直线
点恰好落在直线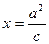 上,则该椭圆的离心率为__________________________
上,则该椭圆的离心率为__________________________