题目内容
选修4﹣4;坐标系与参数方程
已知点P(1+cosα,sinα),参数α∈[0,π],点Q在曲线C: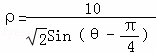 上.
上.
(1)求点P的轨迹方程和曲线的直角坐标方程:
(2)求|PQ|的最小值.
考点:
参数方程化成普通方程;点的极坐标和直角坐标的互化.
专题:
计算题.
分析:
(1)设点P的坐标为(x,y),则有 ![]() ,消去参数α,得到点P的轨迹方程.曲线C 的极坐标方程即
,消去参数α,得到点P的轨迹方程.曲线C 的极坐标方程即
10=![]() (
(![]() sinθ﹣
sinθ﹣![]() cosθ),依据x=ρcosθ,y=ρsinθ,化为直角坐标方程.
cosθ),依据x=ρcosθ,y=ρsinθ,化为直角坐标方程.
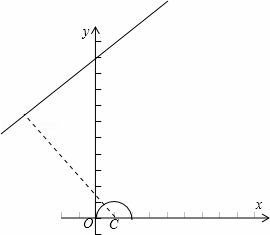
(2)如图,由题意可得点Q在直线x﹣y+10=0 上,点P在半圆上,求出半圆的圆心C到直线的距离,将此距离减去半径1,
即为所求.
解答:
解:(1)设点P的坐标为(x,y),则有 ![]() ,消去参数α,可得:(x﹣1)2+y2=1.
,消去参数α,可得:(x﹣1)2+y2=1.
由于α∈[0,π],∴y≥0,故点P的轨迹是上半圆:(x﹣1)2+y2=1(y≥0).
∵曲线C: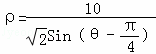 ,即 10=
,即 10=![]() (
(![]() sinθ﹣
sinθ﹣![]() cosθ),
cosθ),
即 ρsinθ﹣ρcosθ=10,故曲线C的直角坐标方程:x﹣y+10=0.
(2)如图所示:由题意可得点Q在直线x﹣y+10=0 上,点P在半圆上,
半圆的圆心C(1,0)到直线x﹣y+10=0的距离等于 ![]() =
=![]() .
.
即|PQ|的最小值为 ![]() .
.
点评:
本题主要考查把参数方程化为普通方程的方法,把极坐标方程化为直角坐标方程的方法,体现了数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
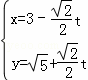 (t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为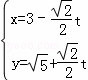 (t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为