题目内容
已知函数f(x)=x2-2,g(x)=xlnx,
(1)若对一切x∈(0,+∞),2g(x)≥ax-5-f(x)恒成立, 求实数a的取值范围;
(2)试判断方程ln(1+x2)-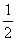 f(x)-k=0有几个实根。
f(x)-k=0有几个实根。
(1)若对一切x∈(0,+∞),2g(x)≥ax-5-f(x)恒成立, 求实数a的取值范围;
(2)试判断方程ln(1+x2)-
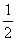 f(x)-k=0有几个实根。
f(x)-k=0有几个实根。 解:(1)若对一切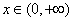 , ,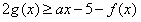 恒成立, 恒成立,即 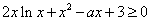 在 在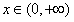 恒成立, 恒成立,∴ 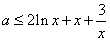 在 在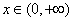 恒成立, 恒成立,令 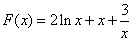 , ,则 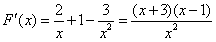 , ,当 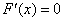 时,x=1,F(x)在(0,1)递减,在(1,+∞)递增, 时,x=1,F(x)在(0,1)递减,在(1,+∞)递增,∴ 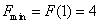 , ,∴只需a≤4。 (2)将原方程化为 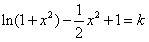 , ,令 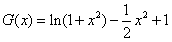 ,G(x)为偶函数,且G(0)=1, ,G(x)为偶函数,且G(0)=1,当x>0时, 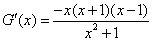 , ,
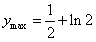 ,且 ,且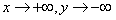 , ,∴当 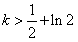 时,无解; 时,无解;当 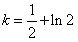 或k=1时,三解; 或k=1时,三解;当 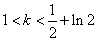 时,四解; 时,四解;当k<1时,两解。 |

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|
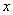
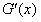
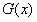
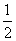 +ln2
+ln2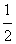 +ln2
+ln2