题目内容
如图,已知AB是圆柱下底面圆O2的直径,PA是圆柱的一条母线,C是圆柱下底面圆O2圆周上一点.
(1)求证:BC⊥平面PAC;
(2)若C恰为弧AB的中点,按图中所给尺寸,计算三棱锥B—PAC的体积.
(1)证明:∵PA是圆柱的一条母线,
∴PA⊥平面APC.而BC
平面ADC,
∴PA⊥BC.
又∵AB是圆柱下底面圆O的直径,C是圆柱底面圆周上一点,
∴BC⊥AC.
又PC∩AC=C,且PC,AC在平面PAC内,
∴BC⊥平面PAC.
(2)解:∵C恰为的中点,
∴△ABC为等腰直角三角形,由(1)知BC为三棱锥B—PAC的高.
由图中所给数据可得AC=BC=20
,
又S△PAC=
PA·AC=600
,
∴VB-PAC=
S△PAC·BC=8 000.
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
如图，已知圆柱的底面半径是3，高是4，A、B两点分别在两底面的圆周上，并且AB=5，那么直线AB与轴OO'之间的距离等于
（2012•青州市模拟）如图，已知平面BCC1B1是圆柱的轴截面（经过圆柱的轴的截面），BC是圆柱底面的直径，O为底面圆心，E为母线CC1的中点，已知AB=AC=AA1=4．
（2012•黄浦区二模）如图，已知圆柱的轴截面ABB1A1是正方形，C是圆柱下底面弧AB的中点，C1是圆柱上底面弧A1B1的中点，那么异面直线AC1与BC所成角的正切值为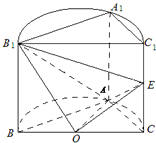
如图，已知平面BCC1B1是圆柱的轴截面（经过圆柱的轴的截面），BC是圆柱底面的直径，O为底面圆心，E为母线CC1的中点，已知AB=AC=AA1=4．