题目内容
关于x的方程2x2+3ax+a2-a=0至少有一个模为1的复数根,则实数a的所有可能值为________.
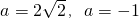
分析:原方程的根是实根与虚根讨论:(1)对于方程 2x2+3ax+a2-a=0 若方程有实根,(2)若方程有共轭复数根,则可设两根为cosθ+isinθ、cosθ-isinθ,分别求出a的值,从而得到答案.
解答:(1)对于方程 2x2+3ax+a2-a=0 若方程有实根,则实根中有一个根为1或-1,
△=9a2-8(a2-a)=a(a+8)≥0,得a≤-8或a≥0,
将x=1代入方程,得2+3a+a2-a=0,即a2+2a+2=0,a无实根;
将x=-1代入方程,得2-3a+a2-a=0,即a2-4a+2=0,得a=2±

(2)若方程有共轭复数根,则可设两根为cosθ+isinθ、cosθ-isinθ,
△=9a2-8(a2-a)=a(a+8)<0,得-8<a<0 由韦达定理,
有 cosθ+isinθ+cosθ-isinθ=2cosθ=-
 a,
a,得cosθ=-
 a,
a,(cosθ+isinθ)(cosθ-isinθ)=cos2θ+sin2θ=1=
 (a2-a),
(a2-a),即(a+1)(a-2)=0,?a=2或a=-1,
a=-1时,cosθ=
 ∈[-1,1];
∈[-1,1];a=2不在-8<a<0的范围内,舍去.
∴a=-1
故答案为:a=2±
 或-1
或-1点评:本小题主要考查一元二次方程的根的分布与系数的关系、复数的三角形式的应用、复数相等等基础知识,考查运算求解能力,考查分类讨论思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
若关于x的方程2x2-3x+m=0的两根满足x1∈(-2,-1),x2∈(2,3),则m的取值范围是( )
A、(-∞,
| ||
| B、(-9,-5) | ||
C、(-14,
| ||
| D、(-14,-2) |