Question

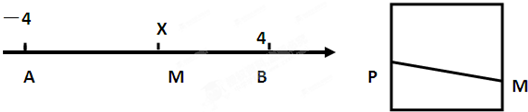
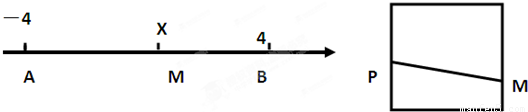
如图，数轴上点A对应的数值为-4，点B对应的数值为4，点M对应的数值为x（-4＜x＜4），现将线段AB弯折成一个边长为2的正方形，使A、B两点重合于点P（P为该边的中点），设线段PM的长度为L，则建立了一个L关于x的映射关系L=L（x），有下列论断：

（1）
（2）L（x）为偶函数
（3）L（x）有3个极值点
（4）L（x）在（-4，4）上为单调函数．
其中正确的个数为_____个．

1. A.
   1
2. B.
   2
3. C.
   3
4. D.
   4

Answer 1

C
分析：由图形可知
（1）通过勾股定理可计算出；
（2）因为PM关于经过正方形的边CE、FD的中点所在的直线对称，故是偶函数；
（3）由表达式可求出其三个极值点0，-1，1；
（4）因为（2）正确，所以（4）不正确．
解答：如图所示：（1）当M为边CD的中点时，由勾股定理得L（2）==，故（1）正确；
（2）由图的对称性可看出L（-x）=L（x）；
（3）当0≤x＜4时，L（-x）=L（x）=，可知当x=0时，L（x）取得极小值；当x=±1时，L（x）取得极大值，故有三个极值点．
（4）由（2）可知L（x）在区间（-4，4）是偶函数，故不是单调函数，所以（4）不正确．
故选C．
点评：正确画出图形是解决问题的关键．