题目内容
(本题满分12分)
对每个正整数n, 是抛物线
是抛物线 上的点,过焦点F的直线FAn交抛物线另一点
上的点,过焦点F的直线FAn交抛物线另一点 。
。
(1)试证:
(2)取 并
并 为抛物线上分别为
为抛物线上分别为 与
与 为切点的两条切线的交点,求证
为切点的两条切线的交点,求证
对每个正整数n,
 是抛物线
是抛物线 上的点,过焦点F的直线FAn交抛物线另一点
上的点,过焦点F的直线FAn交抛物线另一点 。
。(1)试证:

(2)取
 并
并 为抛物线上分别为
为抛物线上分别为 与
与 为切点的两条切线的交点,求证
为切点的两条切线的交点,求证
(1)
 ,证明略。
,证明略。(2)
 ,证明略
,证明略对每个正整数n, 是抛物线
是抛物线 上的点,过焦点F的直线FAn交抛物线另一点
上的点,过焦点F的直线FAn交抛物线另一点 。 (1)试证:
。 (1)试证:
(2)取 并
并 为抛物线上分别为
为抛物线上分别为 与
与 为切点的两条切线的交点,求证
为切点的两条切线的交点,求证
(1)证明:焦点(0,1)设直线AnBn方程为:
 消去y得
消去y得 

(2)由 则
则
 在An处切线方程为
在An处切线方程为
即 ①
①
同理:在Bn处切线方程为: ②
②
①~②两式相减得: 代入可得y="-1 "
代入可得y="-1 " 

 是抛物线
是抛物线 上的点,过焦点F的直线FAn交抛物线另一点
上的点,过焦点F的直线FAn交抛物线另一点 。 (1)试证:
。 (1)试证:
(2)取
 并
并 为抛物线上分别为
为抛物线上分别为 与
与 为切点的两条切线的交点,求证
为切点的两条切线的交点,求证
(1)证明:焦点(0,1)设直线AnBn方程为:

 消去y得
消去y得 

(2)由
 则
则
 在An处切线方程为
在An处切线方程为
即
 ①
① 同理:在Bn处切线方程为:
 ②
②①~②两式相减得:
 代入可得y="-1 "
代入可得y="-1 " 


练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 ,其中
,其中 为2,4,6,8中任取的一个数,
为2,4,6,8中任取的一个数,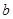 为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线
为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线 交点处的切线相互平行的概率是( )
交点处的切线相互平行的概率是( )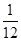



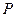 的轨迹
的轨迹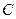 的方程;
的方程;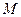 过定点
过定点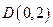 ,圆心
,圆心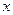 轴交于
轴交于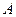 、
、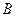 两点,设
两点,设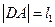 ,
,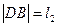 ,求
,求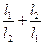 的最大值.
的最大值.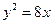 ,
,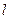 过抛物线的焦点
过抛物线的焦点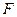 ,且垂直于
,且垂直于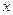 轴,
轴,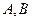 两点,求
两点,求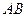 的长度。
的长度。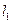 过抛物线的焦点
过抛物线的焦点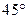 ,直线
,直线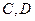 两点,
两点,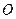 为原点。求△
为原点。求△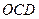 的面积。
的面积。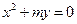 上的点到定点
上的点到定点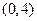 和到定直线
和到定直线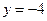 的距离相等,则
的距离相等,则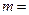
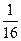 ;
;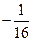 ;
;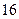 ;
;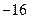 .
.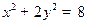 的一个焦点,则此抛物线的焦点到其准线的距离等于是 。
的一个焦点,则此抛物线的焦点到其准线的距离等于是 。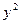 =2px(p>0)的焦点F的
=2px(p>0)的焦点F的 直线
直线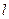 与抛物线在第一象限的交点为A,与抛物线准线的交点为B,点A在抛物线准线上的射影为C,若
与抛物线在第一象限的交点为A,与抛物线准线的交点为B,点A在抛物线准线上的射影为C,若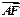 =
=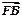 ,
,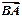 ·
·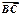 =48,则抛物线的方程为______________。
=48,则抛物线的方程为______________。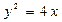 上一点P引抛物线准线的垂线,垂足为
上一点P引抛物线准线的垂线,垂足为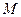 且
且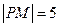 ,设抛物线的焦点为F,则
,设抛物线的焦点为F,则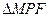 的面积为( )
的面积为( )