题目内容
设a,b为不相等的两个正数，且a3-b3=a2-b2,求证：1＜a+b＜
.
思路分析：分析题意可得，a2+ab+b2=a+b，可用基本不等式进一步放缩得到a+b＞1，化简整理可得,(a+b)2=a2+2ab+b2=a+b+ab＜a+b+，通过放缩达到证明目的.
证明：（1）依题意：a2+ab+b2=a+b，于是(a+b)2＞a2+ab+b2=a+b,
故a+b＞1，又(a+b)2＞4ab，而
(a+b)2=a2+2ab+b2=a+b+ab＜a+b+
,
即
(a+b)2＜a+b,∴a+b＜
.综合上述可得：1＜a+b＜
.
练习册系列答案
相关题目
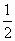[f(x1)＋f(x2)]有不相等的两实根，且必有一根属于(x1、x2)；
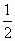[f(x1)＋f(x2)]在(x1、x2)内的实根为m，且x1、m－
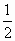、x2成等差数列，设x＝x0是f(x)的对称轴方程．
.
.
.