题目内容
已知集合![]() ,其中
,其中![]() ,
,![]() 表示和
表示和![]() 中所有不同值的个数.
中所有不同值的个数.
(Ⅰ)设集合![]() ,
,![]() ,分别求
,分别求![]() 和
和![]() ;
;
(Ⅱ)若集合![]() ,求证:
,求证:![]() ;
;
(Ⅲ)![]() 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由?
是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由?
解:(Ⅰ)由![]()
得![]() .
.
由![]()
得![]() .----------------------------------------------------------------------------------------------5分
.----------------------------------------------------------------------------------------------5分
(Ⅱ)证明:因为![]() 最多有
最多有![]() 个值,所以
个值,所以![]()
又集合![]() ,
,
任取![]()
当![]() 时,不妨设
时,不妨设![]() ,则
,则![]() ,
,
即![]() .
.
当![]() 时,
时,![]() .
.
因此,当且仅当![]() 时,
时, ![]() .
.
即所有![]() 的值两两不同,
的值两两不同,
所以![]() -----------------------------------------------------------------------------------------9分
-----------------------------------------------------------------------------------------9分
(Ⅲ) ![]() 存在最小值,且最小值为
存在最小值,且最小值为![]() .
.
不妨设![]() 可得
可得
![]()
所以![]() 中至少有
中至少有![]() 个不同的数,即
个不同的数,即![]()
事实上,设![]() 成等差数列,
成等差数列,
考虑![]() ,根据等差数列的性质,
,根据等差数列的性质,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
因此每个和![]() 等于
等于![]() 中的一个,或者等于
中的一个,或者等于![]() 中的一个.
中的一个.
所以对这样的![]() ,所以
,所以![]() 的最小值为
的最小值为![]() . --------------------------------------13分
. --------------------------------------13分

练习册系列答案
相关题目
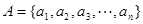 ,其中
,其中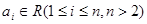 ,
,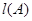 表示和
表示和 中所有不同值的个数.设集合
中所有不同值的个数.设集合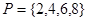 ,则
,则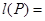 .
.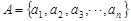 ,其中
,其中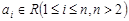 ,
,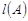 表示
表示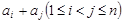 的所有不同值的个数.
的所有不同值的个数.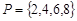 ,
,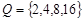 ,分别求
,分别求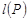 ,
,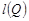 ;
;