题目内容
已知集合![]() ,其中
,其中![]() ,
,![]() 表示和
表示和![]() 中所有不同值的个数.
中所有不同值的个数.
(Ⅰ)设集合![]() ,
,![]() ,分别求
,分别求![]() 和
和![]() ;
;
(Ⅱ)对于集合![]() ,猜测
,猜测![]() 的值最多有多少个;
的值最多有多少个;
(Ⅲ)若集合![]() ,试求
,试求![]() .
.
解:(Ⅰ)由![]()
得![]() .
.
由![]()
得![]() .
.
(Ⅱ)对于集合![]() ,
,![]() 的值最多有
的值最多有![]() 个.
个.
因为在集合![]() 的
的![]() 个元素中任取一个元素,共有
个元素中任取一个元素,共有![]() 种,再从余下的
种,再从余下的![]() 个元素中任取一个元素,
个元素中任取一个元素,
共有![]() 种.把取出的元素两两作和共有
种.把取出的元素两两作和共有![]() 个,考虑到
个,考虑到![]() ,及
,及![]()
等情况,所以对于集合![]() ,
,![]() 的值最多有
的值最多有![]() 个.
个.
(注:本问只要回答正确,就得本问的满分。当然最好能有理由简述,如上。)
(Ⅲ) 因为集合![]() 最多有
最多有![]() 个
个![]() 的值,
的值,
所以![]()
又集合![]() ,任取
,任取![]()
当![]() 时,不妨设
时,不妨设![]() ,则
,则![]() ,即
,即![]() .
.
当![]() 时,
时,![]() .
.
因此,当且仅当![]() 时,
时, ![]() .
.
即所有![]() 的值两两不同,
的值两两不同,
所以![]() -
-

练习册系列答案
相关题目
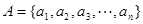 ,其中
,其中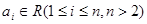 ,
,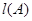 表示和
表示和 中所有不同值的个数.设集合
中所有不同值的个数.设集合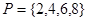 ,则
,则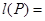 .
.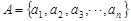 ,其中
,其中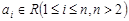 ,
,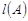 表示
表示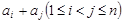 的所有不同值的个数.
的所有不同值的个数.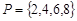 ,
,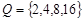 ,分别求
,分别求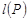 ,
,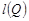 ;
;