题目内容
已知函数 ,数列{an}满足a1=1,当n≥2时,an=f(an-1)
,数列{an}满足a1=1,当n≥2时,an=f(an-1)
(1)求an;
(2)若 ,若Sn=b1+b2+…+bn,求
,若Sn=b1+b2+…+bn,求 .
.
解:(1)∵an=f(an-1)
∴an2+1=2(an-12+1)
∴{an2+1}是以2为首项,2为公比的等比数列
∴an2+1=2n
∴
(2)∵
∴
∴Sn=b1+b2+…+bn=
∴
分析:(1)根据an=f(an-1),可得an2+1=2(an-12+1),从而可知{an2+1}是以2为首项,2为公比的等比数列,故可求an;
(2)由(1)可得 ,从而Sn=b1+b2+…+bn=
,从而Sn=b1+b2+…+bn= ,故可求极限.
,故可求极限.
点评:本题以函数为载体,考查构造法求数列的通项,考查叠加法求和,考查了数列的极限,综合性强.
∴an2+1=2(an-12+1)
∴{an2+1}是以2为首项,2为公比的等比数列
∴an2+1=2n
∴

(2)∵

∴

∴Sn=b1+b2+…+bn=

∴

分析:(1)根据an=f(an-1),可得an2+1=2(an-12+1),从而可知{an2+1}是以2为首项,2为公比的等比数列,故可求an;
(2)由(1)可得
 ,从而Sn=b1+b2+…+bn=
,从而Sn=b1+b2+…+bn= ,故可求极限.
,故可求极限.点评:本题以函数为载体,考查构造法求数列的通项,考查叠加法求和,考查了数列的极限,综合性强.

练习册系列答案
相关题目
 ,数列an满足
,数列an满足 .
.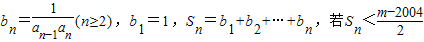 对一切n∈N*成立,求最小正整数m.
对一切n∈N*成立,求最小正整数m.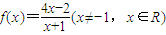 ,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*).
,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*). ,证明数列{bn}是等比数列,并求出通项公式an.
,证明数列{bn}是等比数列,并求出通项公式an. 若数列{an}满足an=
若数列{an}满足an= (n∈N+)且{an}是递减数列,则实数a的取值范围是( )
(n∈N+)且{an}是递减数列,则实数a的取值范围是( ) ,1) B.(
,1) B.(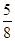 ) C.(
) C.( ) D.(
) D.( ,数列an满足an=f(n)(n∈N*),且an是递增数列,则实数a的取值范围是
,数列an满足an=f(n)(n∈N*),且an是递增数列,则实数a的取值范围是