题目内容
如图,已知双曲线以长方形ABCD的顶点A,B为左、右焦点,且过C,D两顶点.若AB=4,BC=3,则此双曲线的标准方程为 .
【答案】分析:由题意可得点A,B,C的坐标,设出双曲线的标准方程,根据题意知2a=AC-BC,求得a,进而根据b,a和c的关系求得b,则双曲线的方程可得.
解答:解:由题意可得点OA=OB=2,AC=5
设双曲线的标准方程是 .
.
则2a=AC-BC=5-3=2,
所以a=1.
所以b2=c2-a2=4-1=3.
所以双曲线的标准方程是 .
.
故答案为:
点评:本题主要考查了双曲线的标准方程以及直线与椭圆的关系.解答的关键是合理利用双曲线的定义解题.
解答:解:由题意可得点OA=OB=2,AC=5
设双曲线的标准方程是
 .
.则2a=AC-BC=5-3=2,
所以a=1.
所以b2=c2-a2=4-1=3.
所以双曲线的标准方程是
 .
.故答案为:

点评:本题主要考查了双曲线的标准方程以及直线与椭圆的关系.解答的关键是合理利用双曲线的定义解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
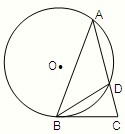 请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.
请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.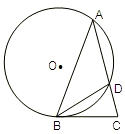 请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.
请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.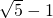 ,求AC的长.
,求AC的长. ,求AC的长.
,求AC的长.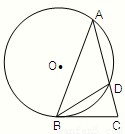
 有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.
有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5. ,过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设l1被圆M截得的弦长为s,l2被圆N截得的弦长为t.
,过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设l1被圆M截得的弦长为s,l2被圆N截得的弦长为t. 是否为定值?请说明理由.
是否为定值?请说明理由.