题目内容
已知数列
满足
,等比数列
为递增数列,且满足
(Ⅰ)求数列的通项公式;
(Ⅱ)令
,不等式
的解集为
,求所有
的和.
（Ⅰ）设的首项为
，公比为
，所以
，解得
…2分
又因为
，所以
则
，
，解得
（舍）或
…………4分
所以
…………6分
（Ⅱ）则
,
当
为偶数，
，即
，不成立
当为奇数，
，即
，
因为
，所以
…………9分
则
组成首项为
，公差为
的等差数列;
组成首项为
，公比为
的等比数列则所有的和为
…………13分
练习册系列答案
相关题目
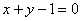且与圆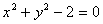
相切的直线的方程是（ ）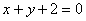
B.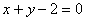 
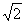=0 或x+y-2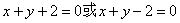
与圆
有且只有三个公共点，则
的取值范围是（ ）
B．
C．
D．
)a<(
是
的充要条件；④
与
是等价的；⑤“
”是“
”成立的充分条件。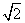
，2
，
，
在
上是增函数，则实数
的范围是
B．
C．