题目内容
 在平行六面体ABCD-A1B1C1D1,已知AB=AD=4,AA1=3,∠A1AB=∠A1AD=∠BAD=
在平行六面体ABCD-A1B1C1D1,已知AB=AD=4,AA1=3,∠A1AB=∠A1AD=∠BAD= ,
,
(1)求AC1的长;
(2)求平行六面体ABCD-A1B1C1D1的体积.
解:(1)记A1在面ABCD内的射影为O,
∵∠A1AB=∠A1AD,∴O在∠BAD的平分线上,
又AB=AD,∴∠BAD的平分线即菱形ABCD的
对角线AC,故O在AC上;∵cos∠A1AB=cos∠A1AO×cos∠OAB
∴cos∠A1AO= ,∴sin∠A1AO=
,∴sin∠A1AO= ,AO=
,AO=
cos∠ACC1=- ;又AC=4
;又AC=4 ,在△ACC1中由余弦定理得AC1=9;
,在△ACC1中由余弦定理得AC1=9;
所以AC1=9;
(2)在△A1AO中,A1O= ,
,
VABCD-A1B1C1D1= =24
=24 .
.
注:求AC1的长还可以用向量: ,平方即可.
,平方即可.
分析:(1)记A1在面ABCD内的射影为O,O在∠BAD的平分线上,说明∠BAD的平分线即菱形ABCD的对角线AC,求AC1的长
(2)求出底面面积,求出高,即可求平行六面体ABCD-A1B1C1D1的体积.
点评:本题考查几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.解题关键在于,正确解三角形.
∵∠A1AB=∠A1AD,∴O在∠BAD的平分线上,
又AB=AD,∴∠BAD的平分线即菱形ABCD的
对角线AC,故O在AC上;∵cos∠A1AB=cos∠A1AO×cos∠OAB
∴cos∠A1AO=
 ,∴sin∠A1AO=
,∴sin∠A1AO= ,AO=
,AO=
cos∠ACC1=-
 ;又AC=4
;又AC=4 ,在△ACC1中由余弦定理得AC1=9;
,在△ACC1中由余弦定理得AC1=9;所以AC1=9;
(2)在△A1AO中,A1O=
 ,
,VABCD-A1B1C1D1=
 =24
=24 .
.注:求AC1的长还可以用向量:
 ,平方即可.
,平方即可.分析:(1)记A1在面ABCD内的射影为O,O在∠BAD的平分线上,说明∠BAD的平分线即菱形ABCD的对角线AC,求AC1的长
(2)求出底面面积,求出高,即可求平行六面体ABCD-A1B1C1D1的体积.
点评:本题考查几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.解题关键在于,正确解三角形.

练习册系列答案
相关题目
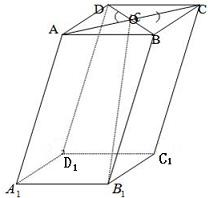
如图,在平行六面体ABCD-A1B1C1D1中,O为AC与BD的交点,若
=
,
=
,
=
,则向量
等于( )
| A1B1 |
| a |
| A1D1 |
| b |
| AA1 |
| c |
| B1O |

A、
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、-
|
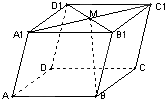 如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若
如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| BM |
A、-
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|
 已知在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,且∠BAD=∠BAA1=∠DAA1=60°,求AC1的长.
已知在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,且∠BAD=∠BAA1=∠DAA1=60°,求AC1的长.