题目内容
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形.
(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC. 
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)先证得 ,
, ,即可得
,即可得 ;(Ⅱ)作
;(Ⅱ)作 ,得
,得 ,再在
,再在 中求解sin∠ANC.
中求解sin∠ANC.
试题解析:(Ⅰ)连接 ,则
,则 ,因为四边形
,因为四边形 是平行四边形,所以
是平行四边形,所以 ∥
∥ ,因为
,因为 是
是 的切线,所以
的切线,所以 ,可得
,可得 ,又因为
,又因为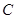 是
是 的中点,所以
的中点,所以 ,得
,得 ,故
,故 . (5分)
. (5分)
(Ⅱ)作 于
于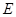 点,则
点,则 ,由(Ⅰ)可知
,由(Ⅰ)可知 ,
,
故 . (10分)
. (10分)
考点:平面几何关系证明.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,锐角三角形ABC的高CD和高BE相交于O,则与△DOB相似的三角形个数是( )
| A.1 | B.2 | C.3 | D.4 |
设圆内两条相交弦,其中一弦长为8 cm,且被交点平分,另一条弦被交点分成1∶4两部分,则这条弦长是
| A.2 cm | B.8 cm | C.10 cm | D.12 cm |
如图所示,经过⊙O上的点A的切线和弦BC的延长线相交于点P,若∠CAP=40°,∠ACP=100°,则∠BAC所对的弧的度数为
| A.40° | B.100° | C.120° | D.30° |
如图所示,若D是 的中点,则与∠ABD相等的角的个数是
的中点,则与∠ABD相等的角的个数是
| A.7 | B.3 |
| C.2 | D.1 |
如图,已知AB∥CD∥EF,AF,BE相交于点O,若AO=OD=DF,BE=10 cm,则BO的长为 ( ).
A. cm cm | B.5 cm |
C. cm cm | D.3 cm |
 B.1 C.2
B.1 C.2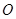 的割线
的割线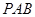 交圆
交圆 、
、 两点,割线
两点,割线 经过圆心
经过圆心 ,
, ,
, ,则圆
,则圆




