题目内容
已知函数f(x)和g(x)的图象关于原点对称，f(x)=x2+2x(Ⅰ)求函数g(x)的解析式；
(Ⅱ)解不等式g(x)≥f(x)-|x-1|．
答案：解：(Ⅰ)因为函数f(x)和g(x)的图象关于原点对称
所以g(x)=-f(-x)=-[(-x)2+2(-x)]=-x2+2x
(Ⅱ)由g(x)≥f(x)-|x-1|可得，2x2-|x-1|≤0
所以，当x≥1时，2x2-x+1≤0，此时不等式无解
当x＜1时，2x2+x-1≤0，解得-1≤x≤
所以，原不等式的解集为[-1，
].
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知函数f(x)和g(x)分别由下表给出定义：
| x | 1 | 2 | 3 |
| f(x) | 2 | ________ | 3 |
| x | 1 | 2 | 3 |
| g(x) | 3 | ________ | 1 |
若方程f(g(x))＝g(f(x))的解恰有2个，请在表中横线上填上合适的数．
；
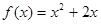
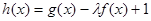在[－1，1]上是增函数，求实数
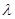的取值范围。