题目内容
设函数f(x)=|2x-4|+1.(Ⅰ)画出函数y=f(x)的图象:
(Ⅱ)若不等式f(x)≤ax的解集非空,求a的取值范围.
【答案】分析:(I)先讨论x的范围,将函数f(x)写成分段函数,然后根据分段函数分段画出函数的图象即可;
(II)根据函数y=f(x)与函数y=ax的图象可知先寻找满足f(x)≤ax的零界情况,从而求出a的范围.
解答: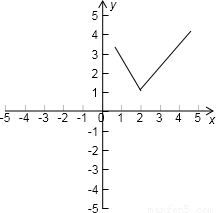 解:(Ⅰ)由于f(x)=
解:(Ⅰ)由于f(x)=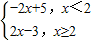 ,
,
函数y=f(x)的图象如图所示.
(Ⅱ)由函数y=f(x)与函数y=ax的图象可知,
当且仅当a<-2或x≥ 时,函数y=f(x)与函数y=ax的图象有交点.
时,函数y=f(x)与函数y=ax的图象有交点.
故不等式f(x)≤ax的解集非空时,
a的取值范围为(-∞,-2)∪[ ,+∞).
,+∞).
点评:本题主要考查了函数的图象,以及利用函数图象解不等式,同时考查了数形结合的数学思想,属于基础题.
(II)根据函数y=f(x)与函数y=ax的图象可知先寻找满足f(x)≤ax的零界情况,从而求出a的范围.
解答:
 解:(Ⅰ)由于f(x)=
解:(Ⅰ)由于f(x)=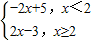 ,
,函数y=f(x)的图象如图所示.
(Ⅱ)由函数y=f(x)与函数y=ax的图象可知,
当且仅当a<-2或x≥
 时,函数y=f(x)与函数y=ax的图象有交点.
时,函数y=f(x)与函数y=ax的图象有交点.故不等式f(x)≤ax的解集非空时,
a的取值范围为(-∞,-2)∪[
 ,+∞).
,+∞).点评:本题主要考查了函数的图象,以及利用函数图象解不等式,同时考查了数形结合的数学思想,属于基础题.

练习册系列答案
相关题目