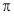题目内容
3.若函数f(x)=x3+mx2+nx+1(m,n∈R)在(-1,1)上单调递减,则m2+n2的取值范围是( )| A. | [$\sqrt{3}$,+∞) | B. | [3,+∞) | C. | (3,+∞) | D. | [9,+∞) |
分析 利用函数的导数,推出m,n的不等式组,然后利用线性规划,表达式的几何意义求解即可.
解答  解:∵f(x)=x3+mx2+nx+1,
解:∵f(x)=x3+mx2+nx+1,
∴f′(x)=3x2+2mx+n,
∵f(x)=x3+mx2+nx+1(m,n∈R)在(-1,1)上单调递减,
∴3x2+2mx+n≤0在区间(-1,1)上恒成立,
∴$\left\{\begin{array}{l}{3-2m+n≤0}\\{3+2m+n≤0}\end{array}\right.$,不等式组表示的可行域如图阴影部分,
∴则m2+n2的几何意义是可行域内的点与原点距离的平方,显然A(0,-3)到原点距离最小,所以则m2+n2≥9.
故选:D.
点评 本题考查函数的单调性,考查导数知识的综合运用,考查学生分析解决问题的能力,线性规划的应用,属于中档题.

练习册系列答案
相关题目
8.已知集合A={x|y=$\sqrt{1-x}$},B={x|x≤2},则( )
| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=(-∞,2] |
10.设直线l与双曲线x2-y2=1的右支相交于M,N两点,与⊙C:(x-4)2+y2=r2(r>0)相切于点P,且P为线段MN的中点,若这样的直线l恰有4条,则r的取值范围是( )
| A. | ($\sqrt{2}$,$\sqrt{6}$) | B. | ($\sqrt{2}$,$\sqrt{7}$) | C. | (2,$\sqrt{6}$) | D. | (2,$\sqrt{7}$) |
 ( )
( ) B.
B. C.
C. D.
D.
 B.24
B.24 C.28
C.28 D.32
D.32