Question

【题目】在如图所示的几何体中，是的中点，.

（1）已知，，求证：平面；

（2）已知分别是和的中点，求证： 平面.

Answer 1

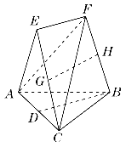
【答案】（1）详见解析；（2）详见解析.

【解析】

试题分析：（1）根据,所以平面就是平面,连接DF,AC是等腰三角形ABC和ACF的公共底边，点D是AC的中点，所以,,即证得平面的条件；（2）要证明线面平行，可先证明面面平行，取的中点为，连接，，根据中位线证明平面平面,即可证明结论.

试题解析：证明：（1）∵，∴与确定平面.

如图①，连结. ∵，是的中点，∴.同理可得.

又，平面，∴平面，即平面.

（2）如图②，设的中点为，连接，.

在中，∵分别是的中点，∴.

又，∴.

在中，∵分别是的中点，∴.

又，∴平面平面.

∵平面，∴平面.