题目内容
设 的内角
的内角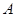 ,
,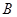 ,
,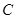 所对的边长分别为
所对的边长分别为 ,
,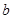 ,
,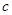 ,且
,且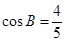 ,
,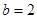 .
.
(1)当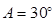 时,求
时,求 的值;
的值;
(2)当 的面积为
的面积为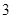 时,求
时,求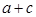 的值.
的值.
(1) ;(2)
;(2) .
.
解析试题分析:(1)先由 计算出
计算出 ,然后根据正弦定理公式
,然后根据正弦定理公式 即可算出
即可算出 的值;(2)先根据
的值;(2)先根据 的面积为3得到
的面积为3得到 ,再结合余弦定理
,再结合余弦定理 得到
得到 ,最后由
,最后由 可计算得结果.
可计算得结果.
试题解析:(1)因为 ,所以
,所以 2分
2分
由正弦定理 ,可得
,可得 4分
4分
所以 5分
5分
(2)因为 的面积
的面积 ,
,
所以 ,
, 7分
7分
由余弦定理
得 ,即
,即 10分
10分
所以 ,
,
所以, 13分.
13分.
考点:1.正弦定理;2.余弦定理;3.三角形的面积计算公式.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
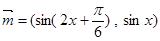 ,
,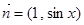 ,
, .
. 的单调递减区间;
的单调递减区间;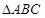 中,
中,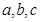 分别是角
分别是角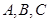 的对边,
的对边, ,
,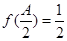 ,
,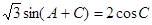 ,求
,求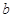 的大小.
的大小. ,点M在线段PQ上.
,点M在线段PQ上.
 ,求PM的长;
,求PM的长; 的图像经过点
的图像经过点 .
. 的值;
的值; 中,
中,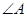 、
、 、
、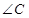 所对的边分别为
所对的边分别为 、
、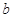 、
、 ,若
,若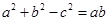 ,且
,且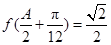 .求
.求 .
. 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按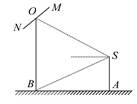
 .
. 的值;
的值; ·
·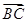 =20,求△ABC的面积.
=20,求△ABC的面积.
 ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值.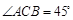 ,求天宁宝塔AB与大楼CD底部之间的距离BD.
,求天宁宝塔AB与大楼CD底部之间的距离BD.