题目内容
甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为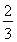 ,乙在每局中获胜的概率为
,乙在每局中获胜的概率为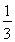 ,且各局胜负相互独立,比赛停止时一共已打
,且各局胜负相互独立,比赛停止时一共已打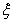 局:
局:
(1)列出随机变量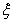 的分布列;
的分布列;
(2)求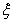 的期望值E
的期望值E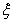 .
.
【答案】
(1)
ξ | 2 | 4 | 6 |
P |
|
|
|
(2)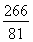
【解析】
试题分析:(1)先列出随机变量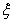 所有可能值,为2,4,6.再分别讨论三种情况下,两者输赢情况,需全面考虑,不能遗漏,如
所有可能值,为2,4,6.再分别讨论三种情况下,两者输赢情况,需全面考虑,不能遗漏,如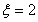 时,甲可以全赢,也可全输,不能一赢一输;
时,甲可以全赢,也可全输,不能一赢一输;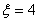 时,前两局必是甲一赢一输;而后两局必是某人全赢;
时,前两局必是甲一赢一输;而后两局必是某人全赢;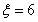 时,可利用概率和为
时,可利用概率和为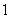 ,求其“补集”即可;也可直接计算,此时需要注意前四局分布情况是:前两局必是甲一赢一输;接下来的两局也必是甲一赢一输,但最后的两局却没有限制;(2)利用期望值计算公式Eξ=2×
,求其“补集”即可;也可直接计算,此时需要注意前四局分布情况是:前两局必是甲一赢一输;接下来的两局也必是甲一赢一输,但最后的两局却没有限制;(2)利用期望值计算公式Eξ=2×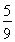 +4×
+4×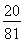 +6×
+6×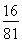 =
=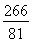
试题解析:解法1:
(1)依题意知,ξ的所有可能值为2,4,6.
设每两局比赛为一轮,则该轮结束时比赛停止的概率为(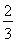 )2+(
)2+(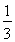 )2=
)2=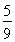 . 4分
. 4分
若该轮结束时比赛还将继续,则甲、乙在该轮中必是各得一分,此时,该轮比赛结果对下轮比赛是否停止没有影响.从在则有
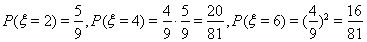 , 7分
, 7分
∴ξ的分布列为
ξ | 2 | 4 | 6 |
P |
|
|
|
9分
(2)Eξ=2×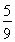 +4×
+4×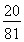 +6×
+6×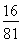 =
=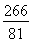 . 12分
. 12分
解法2:(1)依题意知,ξ的所有可能值为2,4,6.
令Ak表示甲在第k局比赛中获胜,则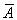 k表示乙在第k局比赛中获胜.
k表示乙在第k局比赛中获胜.
由独立性与互斥性得
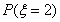 =P(A1A2)+P(
=P(A1A2)+P(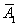
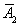 )=
)=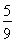 , 2分
, 2分
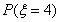 =P(
=P(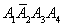 )+P(
)+P(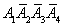 )+P(
)+P(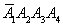 )+P(
)+P(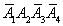 )
)
=2[(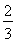 )3(
)3(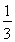 )+(
)+(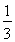 )3(
)3(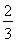 )]=
)]=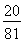 , 4分
, 4分
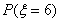 =P(
=P(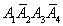 )+P(
)+P(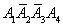 )+P(
)+P(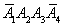 )+P(
)+P(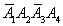 )
)
=4(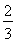 )2(
)2(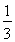 )2=
)2=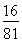 , 7分
, 7分
∴ξ的分布列为
ξ | 2 | 4 | 6 |
P |
|
|
|
9分
(2)Eξ=2×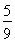 +4×
+4×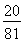 +6×
+6×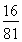 =
=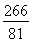 . 12分
. 12分
考点:随机变量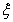 的分布列,期望值
的分布列,期望值

练习册系列答案
相关题目
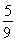
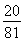
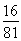
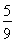
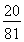
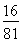
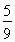
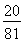
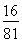
 (2013•辽宁一模)甲乙两人进行乒乓球对抗赛,约定每局胜者得1分,负者得0分,比赛进行到有一个比对方多2分或打满6局时停止.设甲在每局中获胜的概率为P(
(2013•辽宁一模)甲乙两人进行乒乓球对抗赛,约定每局胜者得1分,负者得0分,比赛进行到有一个比对方多2分或打满6局时停止.设甲在每局中获胜的概率为P(