题目内容
设数列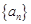 满足
满足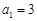 ,
,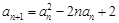 .
.
(1)求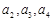 ;
;
(2)先猜想出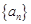 的一个通项公式,再用数学归纳法证明你的猜想.
的一个通项公式,再用数学归纳法证明你的猜想.
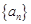 满足
满足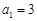 ,
,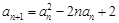 .
.(1)求
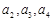 ;
;(2)先猜想出
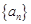 的一个通项公式,再用数学归纳法证明你的猜想.
的一个通项公式,再用数学归纳法证明你的猜想.(1)5,7,9;(2)猜想 ;证明祥见解析.
;证明祥见解析.
 ;证明祥见解析.
;证明祥见解析.试题分析:(1)由已知等式:
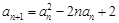 令n=1,再将
令n=1,再将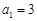 代入即可求得
代入即可求得 的值;再令n=2并将
的值;再令n=2并将 的值就可求得
的值就可求得 的值;最后再令n=2并将
的值;最后再令n=2并将 的值就可求得
的值就可求得 的值;(2)由已知及(1)的结果,可猜想出
的值;(2)由已知及(1)的结果,可猜想出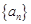 的一个通项公式;用数学归纳法证明时应注意格式:①验证
的一个通项公式;用数学归纳法证明时应注意格式:①验证 时猜想正确;②作归纳假设:假设当
时猜想正确;②作归纳假设:假设当 时,猜想成立,在此基础上来证明
时,猜想成立,在此基础上来证明 时猜想也成立,注意在此证明过程中要充分利用已知条件找出
时猜想也成立,注意在此证明过程中要充分利用已知条件找出 之间的关系,并一定要用到假设当
之间的关系,并一定要用到假设当 时的结论;最后一定要下结论.
时的结论;最后一定要下结论.试题解析: (1)由条件
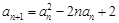 ,依次得
,依次得 ,
,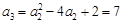 ,
, , 6分
, 6分(2)由(1),猜想
 . 7分
. 7分下用数学归纳法证明之:
①当
 时,
时, ,猜想成立; 8分
,猜想成立; 8分②假设当
 时,猜想成立,即有
时,猜想成立,即有 , 9分
, 9分则当
 时,有
时,有 ,
,即当
 时猜想也成立, 13分
时猜想也成立, 13分综合①②知,数列
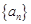 通项公式为
通项公式为 . 14分
. 14分
练习册系列答案
相关题目
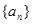 ,满足
,满足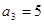 且
且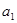 ,
,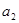 ,
,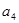 成等比数列.
成等比数列.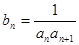 ,求数列
,求数列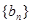 前
前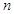 项的和为
项的和为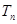 .
.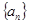 ( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.
( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.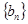 是等差数列;
是等差数列;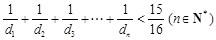 .
.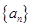 中,
中, 则
则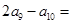 ( )
( ) ,则
,则 的值为( ).
的值为( ).



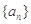 的通项公式
的通项公式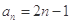 ,设数列
,设数列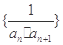 ,其前n项和为
,其前n项和为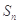 ,则
,则

