Question

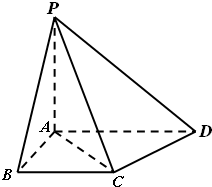（2012•佛山二模）如图所示四棱锥P-ABCD中，PA⊥底面ABCD，四边形ABCD中，AB⊥CD，BC∥AD，PA=AB=BC=2，AD=4．
（1）求四棱锥P-ABCD的体积；
（2）求证：CD⊥平面PAC；
（3）在棱PC上是否存在点M（异于点C），使得BM∥平面PAD，若存在，求

PM

PC

的值；若不存在，说明理由．

Answer 1

分析：（1）利用四边形ABCD是直角梯形，求出S_ABCD，通过PA⊥ABCD底面ABCD，然后求解V_P-ABCD．
（2）证明PA⊥CD，AC⊥CD，通过PA∩AC=A，证明CD⊥PAC
（3）用反证法证明，假设存在点M（异于点C）使得BM∥平面PAD．证明平面PBC∥平面PAD与平面PBC与平面PAD相交，得出矛盾．

解答：解：（1）显然四边形ABCD是直角梯形，
S_ABCD=

1

2

（BC+AD）×AB=

1

2

×（2+4）×2=6
又PA⊥ABCD底面ABCD
∴V_P-ABCD=

1

3

SABCD•PA=

1

3

×6×2=4
（2）∵PA⊥平面ABCD，CD?平面ABCD，∴PA⊥CD
在直角梯形ABCD中，AC=

AB2+BC2

=2

2

，
CD=2

2

，∴AC²+CD²=AD²，即AC⊥CD
又∵PA∩AC=A，
∴CD⊥PAC
（3）不存在，下面用反证法进行证明
假设存在点M（异于点C）使得BM∥平面PAD．
∵BC∥AD，且BC?平面PAD，
AD?平面PAD，
∴BC∥平面PAD
又∵BC∩BM=B，
∴平面PBC∥平面PAD
而平面PBC与平面PAD相交，
得出矛盾．

点评：本题考查直线与平面垂直的判定，棱柱、棱锥、棱台的体积，直线与平面平行的判定的应用，考查空间想象能力，逻辑推理能力．