题目内容
已知1<m<n,m,n∈N*,求证:(1+m)n>(1+n)m.
证明:要证(1+m)n>(1+n)m
只要证nln(1+m)>mln(1+n)
即 >
> .
.
构造函数令f(x)=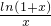 ,x∈[2,+∞],
,x∈[2,+∞],
只要证f(x)在[2,+∞]上单调递减,
只要证f′(x)<0.
∵f′(x)= =
= .
.
当x≥2时,x-lg(1+x)(1+x)<0,
x2(1+x)>0,
∴f′(x)<0,
即x∈[2,+∞]时,f′(x)<0.
以上各步都可逆推,得(1+m)n>(1+n)m.
分析:根据要证明的结论,利用分析法来证明本题,从结论入手,要证结论只要证明后面这个式子成立,两边取对数,构造函数,问题转化为只要证明函数在一个范围上成立,利用导数证明函数的性质.
点评:本题考查不等式的证明,考查化归思想,考查构造函数,是一个综合题,题目难度中等,在证明不等式时,注意采用什么形式,选择一种合适的写法.
只要证nln(1+m)>mln(1+n)
即
 >
> .
.构造函数令f(x)=
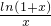 ,x∈[2,+∞],
,x∈[2,+∞],只要证f(x)在[2,+∞]上单调递减,
只要证f′(x)<0.
∵f′(x)=
 =
= .
.当x≥2时,x-lg(1+x)(1+x)<0,
x2(1+x)>0,
∴f′(x)<0,
即x∈[2,+∞]时,f′(x)<0.
以上各步都可逆推,得(1+m)n>(1+n)m.
分析:根据要证明的结论,利用分析法来证明本题,从结论入手,要证结论只要证明后面这个式子成立,两边取对数,构造函数,问题转化为只要证明函数在一个范围上成立,利用导数证明函数的性质.
点评:本题考查不等式的证明,考查化归思想,考查构造函数,是一个综合题,题目难度中等,在证明不等式时,注意采用什么形式,选择一种合适的写法.

练习册系列答案
相关题目