题目内容
下列命题:①|
 |+|
|+| |=|
|=|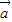 +
+ |是
|是 ,
, 共线的充要条件;
共线的充要条件;②空间任意一点O和不共线的三点A,B,C满足
 =2
=2 +3
+3 -4
-4 ,则P,A,B,C四点共面;
,则P,A,B,C四点共面;③若两个平面的法向量不垂直,则这两个平面一定不垂直.
其中正确的命题的序号是 .
【答案】分析:①| |+|
|+|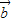 |=|
|=|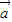 +
+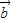 |可推得
|可推得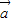 ,
, 共线,但
共线,但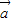 ,
,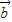 共线,不能推出|
共线,不能推出|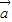 |+|
|+|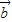 |=|
|=|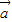 +
+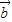 |;②原命题可化为:
|;②原命题可化为: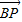 =2
=2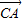 +2
+2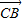 ,可得
,可得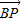 ,
,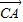 ,
, 共面,进而可得四点共面;③可判其逆否命题正确.
共面,进而可得四点共面;③可判其逆否命题正确.
解答:解:①|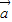 |+|
|+|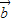 |=|
|=|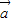 +
+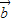 |可推得
|可推得 与
与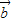 同向或反向,即
同向或反向,即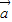 ,
,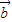 共线,
共线,
但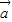 ,
,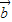 共线,若反向且长度相等,则不能推出|
共线,若反向且长度相等,则不能推出|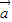 |+|
|+|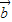 |=|
|=| +
+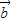 |,故错误;
|,故错误;
②空间任意一点O和不共线的三点A,B,C满足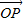 =2
=2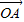 +3
+3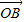 -4
-4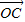 ,
,
则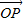 -
-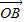 =2
=2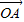 -2
-2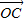 +2
+2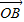 -2
-2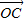 ,即
,即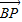 =2
=2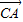 +2
+2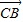
故向量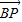 ,
,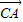 ,
,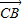 共面,即P,A,B,C四点共面,故正确;
共面,即P,A,B,C四点共面,故正确;
③若两个平面垂直,则它们的法向量一定垂直,由原命题和逆否命题的关系可得
若两个平面的法向量不垂直,则这两个平面一定不垂直,故正确
故答案为:②③
点评:本题考查充要条件的判断,涉及向量的知识的应用,属基础题.
 |+|
|+|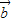 |=|
|=|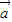 +
+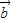 |可推得
|可推得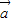 ,
, 共线,但
共线,但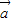 ,
,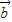 共线,不能推出|
共线,不能推出|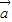 |+|
|+|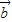 |=|
|=|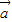 +
+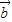 |;②原命题可化为:
|;②原命题可化为: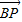 =2
=2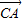 +2
+2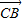 ,可得
,可得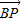 ,
,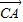 ,
, 共面,进而可得四点共面;③可判其逆否命题正确.
共面,进而可得四点共面;③可判其逆否命题正确.解答:解:①|
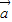 |+|
|+|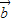 |=|
|=|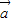 +
+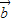 |可推得
|可推得 与
与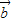 同向或反向,即
同向或反向,即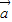 ,
,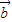 共线,
共线,但
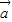 ,
,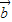 共线,若反向且长度相等,则不能推出|
共线,若反向且长度相等,则不能推出|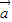 |+|
|+|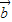 |=|
|=| +
+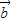 |,故错误;
|,故错误;②空间任意一点O和不共线的三点A,B,C满足
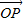 =2
=2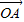 +3
+3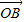 -4
-4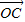 ,
,则
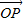 -
-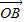 =2
=2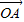 -2
-2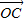 +2
+2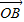 -2
-2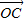 ,即
,即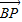 =2
=2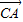 +2
+2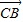
故向量
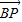 ,
,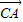 ,
,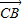 共面,即P,A,B,C四点共面,故正确;
共面,即P,A,B,C四点共面,故正确;③若两个平面垂直,则它们的法向量一定垂直,由原命题和逆否命题的关系可得
若两个平面的法向量不垂直,则这两个平面一定不垂直,故正确
故答案为:②③
点评:本题考查充要条件的判断,涉及向量的知识的应用,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目