题目内容
二次函数f(x)满足f(-2)=-1,f(-1)=-1,且f(x)的最大值是8.(1)求f(x);
(2)求不等式f(x)>-35x2-(108+3m)x+2m2-73(m∈R)的解集.
【答案】分析:(1)利用二次函数的性质即可求出;
(2)通过对m分类讨论即可求出一元二次不等式的解集.
解答:解:(1)设f(x)=ax2+bx+c(a≠0),
∵f(x)满足f(-2)=-1,f(-1)=-1,且f(x)的最大值是8.
∴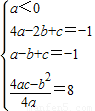 ,解得
,解得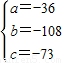 ,
,
∴f(x)=-36x2-108x-73.
(2)由(1)知不等式f(x)>2m2-35x2-(108+3m)x-73(m∈R)等价于
-36x2-108x-73>-35x2-(108+3m)x-73+2m2,
化为x2-3mx+2m2<0,
∴(x-m)(x-2m)<0,
当m=0时,所求不等式的解集为空集;
当m>0时,所求不等式的解集为{x|m<x<2m};
当m<0时,所求不等式的解集为{x|2m<x<m}.
点评:熟练掌握二次函数的性质和分类讨论的方法解一元二次不等式是解题的关键.
(2)通过对m分类讨论即可求出一元二次不等式的解集.
解答:解:(1)设f(x)=ax2+bx+c(a≠0),
∵f(x)满足f(-2)=-1,f(-1)=-1,且f(x)的最大值是8.
∴
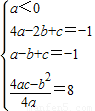 ,解得
,解得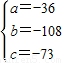 ,
,∴f(x)=-36x2-108x-73.
(2)由(1)知不等式f(x)>2m2-35x2-(108+3m)x-73(m∈R)等价于
-36x2-108x-73>-35x2-(108+3m)x-73+2m2,
化为x2-3mx+2m2<0,
∴(x-m)(x-2m)<0,
当m=0时,所求不等式的解集为空集;
当m>0时,所求不等式的解集为{x|m<x<2m};
当m<0时,所求不等式的解集为{x|2m<x<m}.
点评:熟练掌握二次函数的性质和分类讨论的方法解一元二次不等式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目