题目内容
已知
＝(1，2sinx)
＝(
cos2x，－cosx)设函数f(x)＝
·
．
(1)若x
，求f(x)的最大值、最小值并求出对应的x值；
(2)求f(x)在区间[－π，0]的递减区间．
答案：
解析：
提示：
解析：
|
解：(1)f(x)＝ (2) |
cosx－2sinx·cosx＝
cosx－sin2x＝2cos(2x＋
)．
，
提示：
|
分析：(1)利用三角公式化简表达式，求最值时注意定义域． (2)简单的复合函数的单调区间的求法． 说明：近两年江苏试题没有向量与三角的解答题，而其它省市多以这样的题目作为解答题的第1题，而三角公式、函数的图象及性质也是命题重点，因这样的目的出此题． |
练习册系列答案
相关题目
＝(2cosθ，2sinθ)．θ∈(
，π)，
＝(0，－1)．则
与
夹角是
－θ
＋θ
，π)，若a·b＝
，则tan(α＋
)的值是
，π)，a·b＝
，求cos(α＋
)的值．
＝(sin(ωx－
)，1)，
＝(2sin(ωx＋
)，1)，函数f(x)＝
，求
．
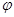）（ω＞0，0＜
＝
，且a∈（0，
），求f（a）的值．