Question

已知A，B，E三点在平面α内，点C，D在α外，并且AC⊥α，DE⊥α，BD⊥AB．若AB=3，AC=BD=4，CD=5，则BD与平面α所成的角等于

30°

．

Answer 1

分析：先确定∠DBE是直线BD与平面α所成的角，然后过点D作DF⊥AC于F，连接AD，AE，可以证明出四边形AEDF为矩形，从而DE=AF．利用勾股定理计算出AD=5=CD，从而得到DF是△ACD的中线，进而在Rt△BDE中，利用三角函数的定义，可得结论．

解答：解：∵DE⊥α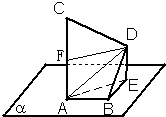，∴BE即为BD在平面α内的射影，∴∠DBE是直线BD与平面α所成的角
过点D作DF⊥AC于F，连接AD，AE
∵AC⊥α，DE⊥α，
∴AC∥DE，且∠AED=∠FAE=∠DFA=90°
∴四边形AEDF为矩形
∴DE=AF
∵BD⊥AB，∴Rt△ABD中，AD=

AB2+BD2

=5
∵△ACD中，CD=AD=5，∴DF是中线，即AF=CF=

1

2

AC=2
∴Rt△BDE中，BD=4，DE=2
∴sin∠DBE=

DE

DB

=

1

2

∴∠DBE=30°，即直线BD与平面α所成的角等于30°
故答案为：30°

点评：本题考查直线与一个平面所成角，考查直线与平面垂直的性质、直线与平面所成角的定义和直角三角形中求三角函数值等知识点，属于中档题．