题目内容
21.
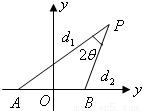
设动点P到点A(-l,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2 sin2θ=λ.
(1)证明:动点P的轨迹C为双曲线,并求出C的方程;
(2)过点B作直线交双曲线C的右支于M、N两点,试确定λ的范围,使![]() ·
·![]() =0,其中点O为坐标原点.
=0,其中点O为坐标原点.
解法一:(1)在△PAB中,![]() ,则
,则![]() ,
,
4=(d1-d2)2+4d1d2sin2![]() ,即
,即![]() (常数),
(常数),
点P的轨迹C是以A、B为焦点,实轴长![]() 的双曲线,方程为:
的双曲线,方程为:![]() .
.
(2)设M(x1,y1),N(x2,y2)
①当MN垂直于x轴时,MN的方程为x=1,M(1,1),N(1,-1)在双曲线上,
即![]() ,因为
,因为![]() ,所以
,所以![]() .
.
②当MN不垂直于x轴时,设MN的方程为y=k(x-1).
由 得
得![]() ,
,
由题意知:![]() ,所以
,所以![]() ,
,![]() ,
,
于是![]() ,
,
因为![]() ,且M,N在双曲线右支上 所以
,且M,N在双曲线右支上 所以
 ,
,
由①②知![]() 。
。
解法二:(1)同解法一
(2)设M(x1,y1),N(x2,y2),MN的中点为E(x0,y0).
①当x1=x2=1时,![]() ,因为
,因为![]() 所以
所以![]() ;
;
②当![]() 时,
时, .
.
又![]() .所以
.所以![]() ;
;
由![]() 得
得![]() ,由第二定义得
,由第二定义得![]()
=![]() ,
,
所以![]() .
.
于是由 得
得![]()
因为x0>1,所以![]() ,又
,又![]()
解得:![]() .由①②知
.由①②知![]() .
.

练习册系列答案
相关题目
 设动点P到点A(-1,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2sin2θ=λ.
设动点P到点A(-1,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2sin2θ=λ.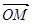 ·
·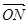 =0,其中点
=0,其中点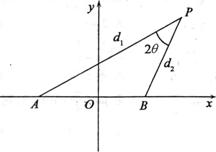
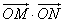 =0,其中点O为坐标原点.
=0,其中点O为坐标原点.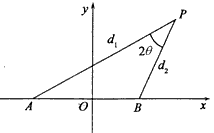
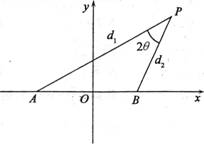 设动点P到点A(-l,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2 sin2θ=λ.
设动点P到点A(-l,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2 sin2θ=λ.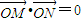 ,其中点O为坐标原点.
,其中点O为坐标原点.