题目内容
设虚数z满足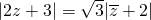 .
.
(1)求证:|z|为定值.
(2)是否存在实数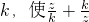 为实数?若存在,求出a的值;若不存在,说明理由.
为实数?若存在,求出a的值;若不存在,说明理由.
(1)依题意,设z=x+yi(x,y∈R,y≠0)…2′
代入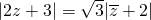 得|(2x+3)+2yi|=
得|(2x+3)+2yi|= |(x+2)-yi|,
|(x+2)-yi|,
整理得:x2+y2=3,即|z|= …6′
…6′
(2)设存在实数k,使得 为实数,
为实数,
则 =
=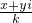 +
+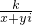
=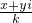 +
+
=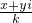 +
+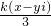
=( +
+ )+(
)+(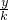 -
- )i∈R,
)i∈R,
∴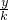 -
- =0,
=0,
∵y≠0,
∴k=± .
.
故存在实数k且k=± ,使
,使 为实数…12′
为实数…12′
分析:(1)设z=x+yi(x,y∈R,y≠0),代入已知条件,可得|z|= ;
;
(2)设存在实数k,使得 为实数,利用复数的模的性质将
为实数,利用复数的模的性质将 化为:(
化为:( +
+ )+(
)+(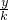 -
- )i∈R,从而得到
)i∈R,从而得到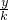 -
- =0,继而可求得k的值.
=0,继而可求得k的值.
点评:本题考查复数代数形式的混合运算,设z=x+yi(x,y∈R,y≠0)代入条件关系式是突破口,着重考查复数模的性质,属于中档题.
代入
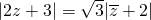 得|(2x+3)+2yi|=
得|(2x+3)+2yi|= |(x+2)-yi|,
|(x+2)-yi|,整理得:x2+y2=3,即|z|=
 …6′
…6′(2)设存在实数k,使得
 为实数,
为实数,则
 =
=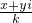 +
+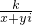
=
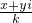 +
+
=
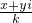 +
+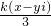
=(
 +
+ )+(
)+(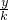 -
- )i∈R,
)i∈R,∴
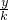 -
- =0,
=0,∵y≠0,
∴k=±
 .
.故存在实数k且k=±
 ,使
,使 为实数…12′
为实数…12′分析:(1)设z=x+yi(x,y∈R,y≠0),代入已知条件,可得|z|=
 ;
;(2)设存在实数k,使得
 为实数,利用复数的模的性质将
为实数,利用复数的模的性质将 化为:(
化为:( +
+ )+(
)+(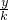 -
- )i∈R,从而得到
)i∈R,从而得到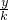 -
- =0,继而可求得k的值.
=0,继而可求得k的值.点评:本题考查复数代数形式的混合运算,设z=x+yi(x,y∈R,y≠0)代入条件关系式是突破口,着重考查复数模的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
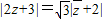 .
.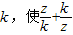 为实数?若存在,求出a的值;若不存在,说明理由.
为实数?若存在,求出a的值;若不存在,说明理由.