题目内容
如图，A，B，C是直线l上不同的三个点，点P不在直线l上，x，y为实数，则使| PC |
| PA |
| PB |
分析：由于A，B，C是直线l上不同的三个点，得出
=λ
，即
-
=λ(
-
)化简即得：
= -
+
，对照条件
=x
+y
即可得出结论．
| AB |
| BC |
| PB |
| PA |
| PC |
| PB |
| PC |
| 1 |
| λ |
| PA |
| 1+λ |
| λ |
| PB |
| PC |
| PA |
| PB |
解答：解：∵A，B，C是直线l上不同的三个点，
∴
=λ
即
-
=λ(
-
)
∴
= -
+
又
=x
+y
∴x+y=1（xy≠0）．反之也成立．
故答案为：x+y=1（xy≠0）．
∴
| AB |
| BC |
即
| PB |
| PA |
| PC |
| PB |
∴
| PC |
| 1 |
| λ |
| PA |
| 1+λ |
| λ |
| PB |
又
| PC |
| PA |
| PB |
∴x+y=1（xy≠0）．反之也成立．
故答案为：x+y=1（xy≠0）．
点评：本小题主要考查充要条件、平面向量基本定理、向量共线等基础知识，考查运算求解能力与转化思想．属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
如图，在三棱锥A-BOC中，AO⊥面BOC，二面角B-AO-C是直二面角，OB=OC，
如图：五面体A-BCC1B1中，AB1=4，△ABC 是正三角形，AB=2，四边形 BCC1B1是矩形，二面角A-BC-C1为直二面角，D为AC的中点．
如图，△A′B′C′是水平放置的△ABC的斜二测直观图，其中O′C′=O′A′=1，O′B′=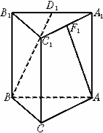
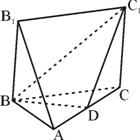（1）求证：AB1∥面BDC1；（2）求二面角C－BC1－D的大小；
.